4Week 39
4.1 Readings for this week's lectures
Sections 14.2-14.3 og 14.6 in the textbook.4.2 Readings for this week's exercises
Sections 7.3, 7.12 and 14.1 in the textbook.4.3 Notes
Differentiation of the inverse function
If is the inverse function to , its derivative is given by
L'Hôpital's rule
If , ,
and , then l'Hôpital's rule can be applied:
Even if and are not defined in the general version of
l'Hôpital's rule can be applied:
This is also valid when the limits are .
4.4 Exercises
A function is given by the expression for .
Assume that the inverse function of exists. Find the derivative for the inverse function, in the point
.
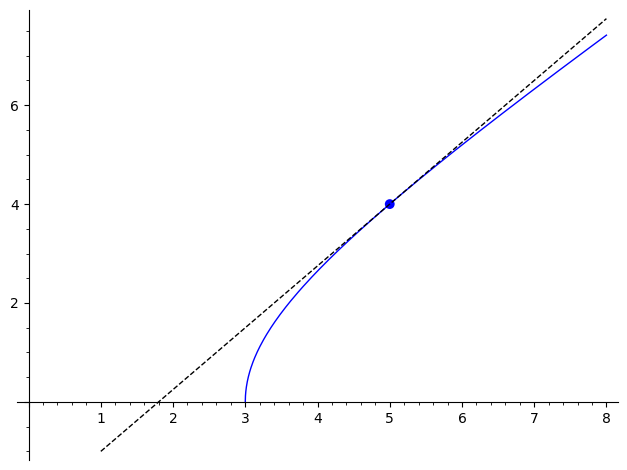
A function has the graph shown below. In the point the function
has a tangent described by the equation . Find the value of
the derivative of the inverse function at .

Answer the questions below, given .
- Calculate the value of for using .
- Find an explicit expression for the inverse function .
- Find an expression for and calculate .
- Did you get the same results in question 1 and 3?
Calculate the limits below.
Can l'Hôpital's rule be applied to calculate this limit?
If yes, find the limit.
Calculate the limit
Notice that you have seen this limit before in exercise 2.9.
Here we look at the probability that two persons in a group of people have their birthday on the same date. We are interested in how this probability changes as a function of the number of people in the group, .Assuming there are 365 days in a year and that all dates are equally likely as a birthday, the probability that two people have their birthday on the same date, , can be approximated asThe function is shown in the plot below.

Show that the amount dough needed for a cylindrical pizza with radius and
thickness can be written as the following function of two variables.
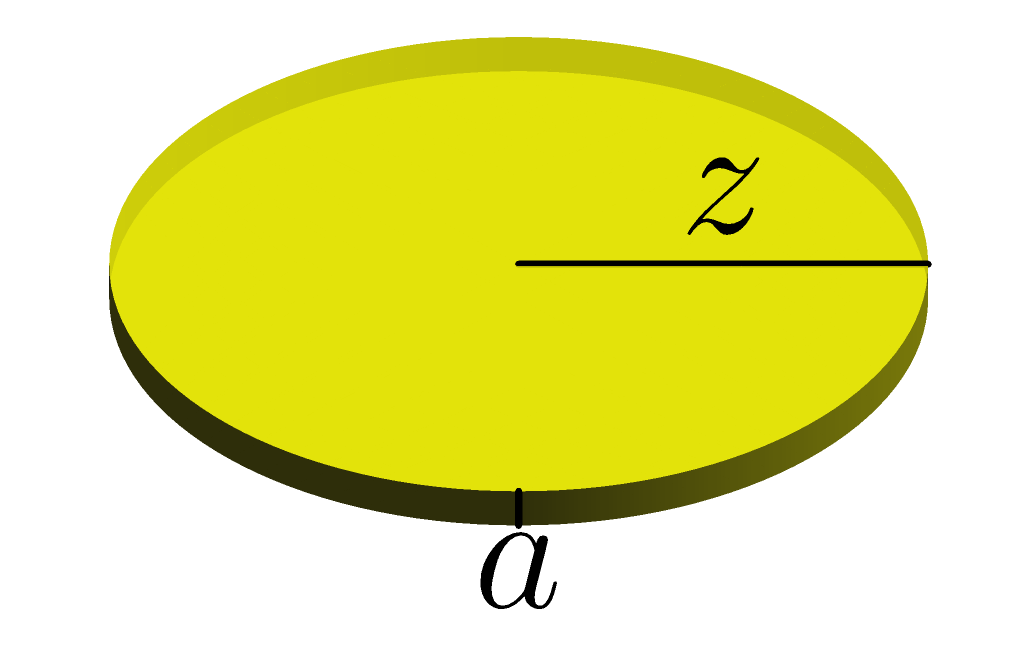
Given the function above, answer the following questions. It is natural to express the answers to the first two questions in units of (yes, that's units of pie!)
First, find the area of the circle that is the top and bottom of the pizza.
Fun fact
Next, multiply by the thickness to obtain the volume.
Note that this formula can be pronounced pizza: .
- How much dough is needed for a (Chicago style) pizza with a radius of 10 cm and a thickness of 1 cm?
- How much dough is needed for a pizza (perhaps from New York or Naples) with a radius of 20 cm and a thickness of 2 mm?
- If the thickness is doubled, by what factor is the amount of dough multiplied?
- If the radius is doubled, by what factor is the amount of dough multiplied?
- Show that and determine the value of .
What is the natural domain of the function ?

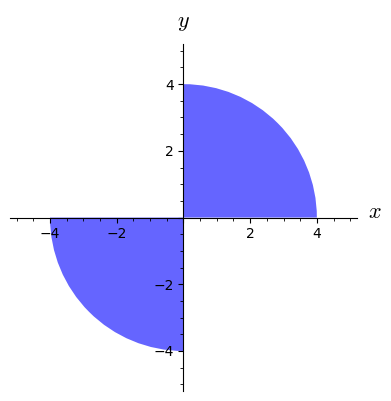


What is the natural domain of the function ?
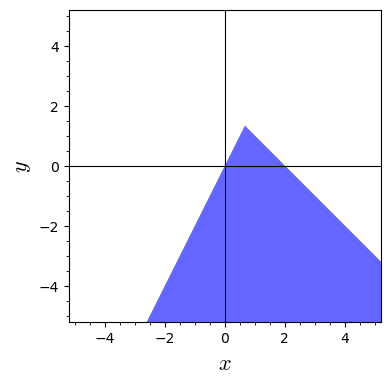


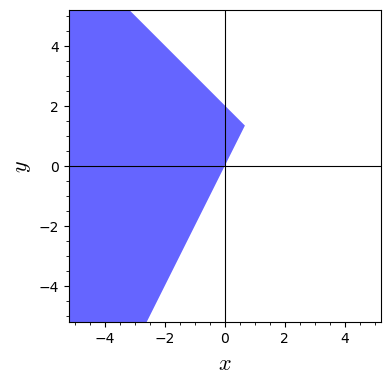
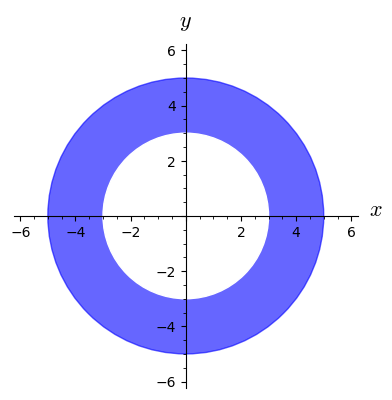
Which of the functions below have the set shown below as the domain?

A function of two variables is given by the expression
- What is the domain for ?
- Sketch the domain.
- Calculate the function values and . Can they all be computed? If not, why not?