13Week 48

13.1 Readings for this week's lectures

Sections 12.6–12.7 and 13.1 in the textbook.

13.2 Readings for this week's exercises

Sections 10.7, 12.1 – 12.3, 12.5 in the textbook.

13.3 Notes

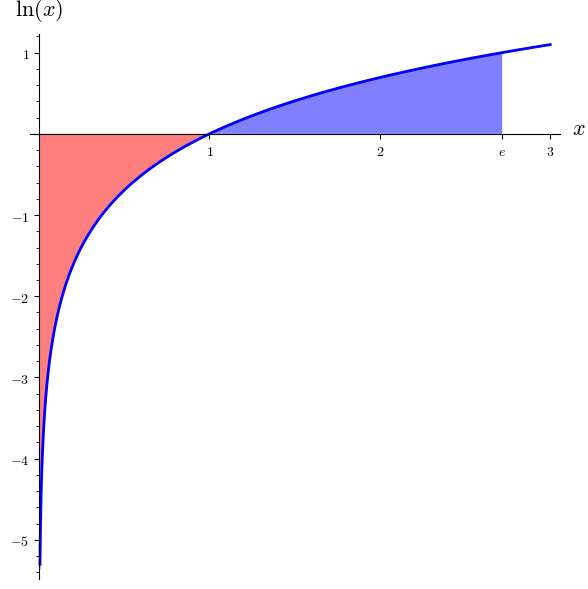
Unbounded limits of integration

A definite integral with $\pm \infty$ as the upper or lower limit is called an improper integral and is defined by the limit:

$\int_a^\infty f(x)\, dx = \lim_{b\to\infty}\int_a^b f(x)\, dx$

$\int_{-\infty}^b f(x)\, dx = \lim_{a\to -\infty}\int_a^b f(x)\, dx$

If the limit exists (and is finite) the integral is convergent and in the opposite case it is divergent.

Unbounded limits of integration

If $f(x)$ is continuous in $]a,b]$ , but $f(x)$ is undefined in $a$ , the definite integral is defined as:

$\int_a^b f(x)\, dx = \lim_{h\to 0^+} \int_{a+h}^b f(x)\, dx$ If the limit exists (and is finite) the integral is said to be convergent, and otherwise divergent.

13.4 Problems

(Previous exam problem)

Calculate the integral:

$\int_0^1 \frac{e^x}{(x+1)^{-2}}\, {\mathrm{d}}x$

(Previous exam problem)

Evaluate the following integral: $\displaystyle \int_0^1 (e^x+e^{-x})^2\, {\mathrm{d}}x$
Evaluate the following integral: $\displaystyle \int \frac{w}{(1-w)^3}\, {\mathrm{d}}w$

Determine the following integral:

$\displaystyle\int_{-\infty}^0 e^x \, dx$

In some valuation models homes are valued at the present value of the saved rent from the time of purchase $(t=0)$ and forever thereafter.

Let $c$ be the yearly saved rent (in millions) and $r$ the interest rate as a decimal number. The value, $V,$ of a home can then be calculated as:

$V = \int_0^{\infty} c e^{-rt} \, dt, \tag{13.1}$

Allan has made a lot of money by building dog runs for his neighbors and considers buying a house that he can let out for 100 000 a year, and he expects the interest rate to be 5%. According to the model (13.1), what is the value of the house?

Determine the following integral:

$\displaystyle\int_1^{\infty} \frac{1}{x^3} \, dx$

Determine the following integral:

$\displaystyle\int_1^{\infty} \frac{1}{\sqrt{x}} \, dx$

(Previous exam problem)

Calculate the integral:

$\displaystyle\int_1^{\infty} \frac{3}{x^2} \, dx$

Consider the integral:

$\int_0^{\infty} k e^{-kx} \, dx, \tag{13.2}$

where $k$ is an arbitrary constant. For which values of $k$ is the integral divergent?

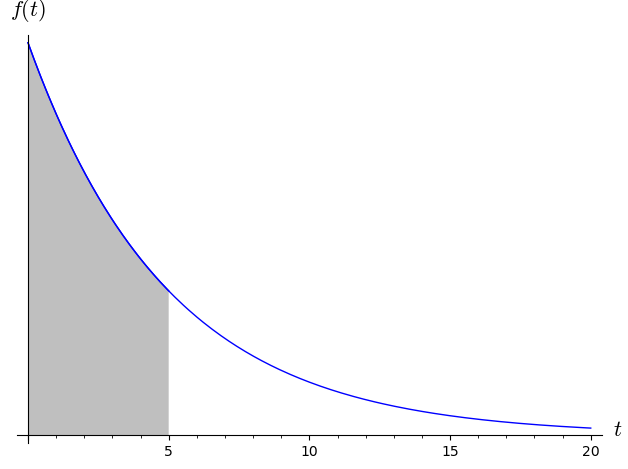
(Previous exam problem)

A store has been provided with a model for the probability of how long it takes between customers arriving at the cash register. The time, in minutes, between customers is $t$ and the model has a probability density, $f(t)$ , given by the function

$f(t) = \lambda e^{-\lambda t}, \qquad t \ge 0,$ where $\lambda$ is a positive constant, that is a parameter in the model. The probability that a new customer arrives within five minutes after the previous customer is given by the shaded area in the figure below.

Find the indefinite integral of $f(t)$ .
The cumulative probability distribution is given by a particular indefinite integral, $F(t)$ , of $f(t)$ , namely, the one that satisfies $F(0) = 0$ . Use this information to determine the constant of integration and therefore also $F(t)$ .
Calculate the probability that a new customer arrives within five minutes after the previous customer.

Determine the values of the definite integrals below.

$\displaystyle \int_{0}^{1} \frac{1}{x} \, {\mathrm{d}}x$
$\displaystyle \int_{0}^{1} \frac{1}{x^3} \, {\mathrm{d}}x$
$\displaystyle \int_{0}^{1} \frac{1}{\sqrt[3]{x}} \, {\mathrm{d}}x$

Consider the definite integral

$\int_{0}^{e} \ln(x) \, {\mathrm{d}}x$

The figure below illustrates the integral.

What happens to the integrand when $x \to 0$ ?
Determine the value of the integral.

Remember that " $0 \cdot \infty$ " is undefined.
Use l'Hôpital's rule.
Use the identity $x \ln x = \frac{\ln x}{x^{-1}}$ .