15Week 50

15.1 Readings for this week's exercises

Read sections 13.2, 13.4, and 13.6 in the textbook.

15.2 Notes

The transpose

Transposition is an operation that swaps rows and columns of a matix. The result of transposing $\mathbf{A}$ is called the transpose of $\mathbf{A}$ , and is written $\mathbf{A}'$ (or $\mathbf{A}^\text{T}$ ).

$\mathbf{A} = \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{pmatrix} \qquad \mathbf{A'} = \begin{pmatrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \end{pmatrix}$

Note: For non-quadratic matrices $\mathbf{A}$ and $\mathbf{A}'$ have different dimensions.

The determinant

The denominator in the solution for $x_1$ and $x_2$ is composed entirely of elements from $\mathbf{A}$ . It is called $\mathbf{A}$ 's determinant, and must be $\neq 0.$

$\det\mathbf{A} = \vert\mathbf{A}\vert = \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix} =a_{11}a_{22}-a_{21}a_{12}$

If $\vert\mathbf{A}\vert \neq 0$ the system has exactly one solution. If $\vert\mathbf{A}\vert = 0$ there are either 0 or $\infty$ many solutions.

Cramer's rule

The numerators in the solutions for $x_1$ and $x_2$ can be written as determinants:

$x_1 = \frac{ \begin{vmatrix} b_{1} & a_{12} \\ b_{2} & a_{22} \end{vmatrix} }{\vert\mathbf{A}\vert} \qquad x_2 = \frac{ \begin{vmatrix} a_{11} & b_{1} \\ a_{21} & b_{2} \end{vmatrix} }{\vert\mathbf{A}\vert}$

This is Cramer's rule for 2 equations with 2 unknowns ( $n=2$ ).

The inverse matrix

The inverse matrix of $\mathbf{A}$ is written $\mathbf{A}^{-1}$ and is defined by

$\mathbf{A}^{-1}\mathbf{A} = \mathbf{A}\mathbf{A}^{-1} = \mathbf{I}$

Only quadratic matrices have an inverse, and only if

$\vert\mathbf{A}\vert\neq 0$

We write a system of $n$ equations with $n$ unknowns as the matrix equation:

$\mathbf{Ax=b}$ If we know the inverse matrix of $\mathbf{A}$ then we can solve the equation as

$\mathbf{x}=\mathbf{A}^{-1}\mathbf{b}$

This is the solution by matrix inversion. Then, we can find the inverse of a $2\times 2$ matrix:

Let

$\mathbf{A} = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}$ If $\vert\mathbf{A}\vert \neq 0$ , then

$\mathbf{A}^{-1} = \frac{1}{\vert\mathbf{A}\vert} \begin{pmatrix} a_{22} & -a_{12} \\ -a_{21} & a_{11} \end{pmatrix}$ Note: we can find the inverse of a $3\times 3$ matrix or higher, but it is more complicated.

15.3 Problems

Find the transpose of the following matrices: $\textbf{A} = \begin{pmatrix} 3 & -8 \\ 1 & \phantom{-}6 \\ 4 & -9 \end{pmatrix}$ , $\textbf{B} = \begin{pmatrix} 0 \\ 1 \\ 1 \\ 7 \end{pmatrix}$ , and $\textbf{C} = \begin{pmatrix} 2 & -3 & 5 & 9 \end{pmatrix}.$

Show that the matrices $\textbf{A} = \begin{pmatrix} 3 & \phantom{-}2 & 3 \\ 2 & -1 & 1 \\ 3 & \phantom{-}1 & 0 \end{pmatrix}$ and $\textbf{B} = \begin{pmatrix} 0 & 4 & 8 \\ 4 & 0 & 13 \\ 8 & 13 & 0 \end{pmatrix}$ are both symmetric.

Denmark, Norway and Sweden have a significant trade with each other. All countries buy goods and services from each other (import) and sell goods and services to each other (export).

Their trade can be expressed in terms of a matrix $\textbf{A}$ , where $\textbf{A} = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}.$

Here, $a_{ij}$ quantifies how much country $i$ exports to country $j$ in billions of kr. For example, if $a_{13}=5$ , then country 1 exports goods and services worth 5 billion kr to country 3.

What are the values of the diagonal elements (where $i=j$ ) in $\textbf{A}$ ?
Is it a fair assumption to make that $\textbf{A}$ is symmetric? Explain your answer.
The minister of trade in country 1 requests a column vector with three elements where element number indicates the total value of the trade between country 1 and country (both import and export). Which of the expressions below will result in such a vector? Explain your answer.
- $2\textbf{A}$
- $\textbf{A}'$
- $(\textbf{A} + \textbf{A}') \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$
- $(\textbf{A} + \textbf{A}')$
- $\textbf{A}\textbf{A}'$
- $(\textbf{A} + \textbf{A}') \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}$

Find the value of the determinant: $\begin{vmatrix} 4 & 6 \\ 2 & 0 \end{vmatrix}$

Find the value of the determinant: $\begin{vmatrix} 8 & 9 \\ 5 & 4 \end{vmatrix}$

Consider the following three systems of two equations with two unknowns:

$\begin{aligned} 2x + 3y & = 3 \\ x - y & = - 1 \end{aligned}\tag{15.1}$

$\begin{aligned} 3x + 2y + 1 & = 0 \\ -\tfrac{3}{2}x - y & = - 2 \end{aligned}\tag{15.2}$

$\begin{aligned} y - \tfrac{2}{3}x & = 2 \\ 4x - 6y + 12 & = 0 \end{aligned}\tag{15.3}$

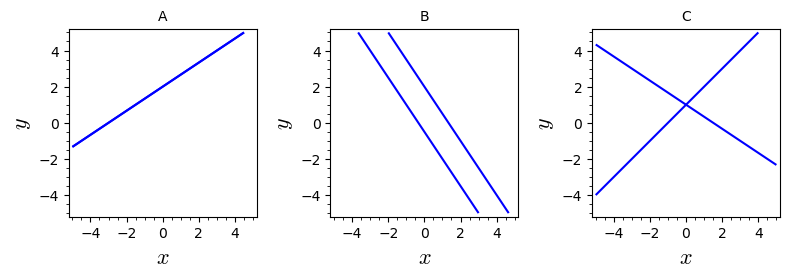
Write each of the three systems of equations in matrix form $\mathbf{Ax} = \mathbf{b}$ .
Calculate $\vert\mathbf{A}\vert$ for each of the three systems of equations.
Indicate which of the plots below corresponds to each of the three systems of equations.
How many solutions are there to each of the three systems of equations?

Use Cramer's rule to solve the system of equations, if possible:

$\begin{aligned} 3x-8y & = 8 \\ x-2y & = 5 \end{aligned}$

Use Cramer's rule to solve the system of equations, if possible:

$\begin{aligned} x+3y & = 1 \\ 3x-2y & = 14 \end{aligned}$

(Previous exam problem) Let $a$ and $b$ be parameters. Use Cramer's rule to solve the following system of equations for the two unknown variables, $x$ and $y$ :

$\begin{aligned} ax-by & = 1 \\ bx+ay & = 2 \end{aligned}$

(Previous exam problem)

Three matrices $\mathbf{A}$ , $\mathbf{B}$ and $\mathbf{C}$ are given by

$\mathbf{A} = \left(\begin{array}{rr} 0 & -1 \\ 1 & 0 \end{array}\right), \qquad \mathbf{B} = \left(\begin{array}{rr} -1 & 0 \\ 0 & -1 \end{array}\right), \qquad \mathbf{C} = \left(\begin{array}{rr} 0 & 1 \\ -1 & 0 \end{array}\right).$

Show that $\mathbf{AB} = \mathbf{C}$ and $\mathbf{BC} = \mathbf{A}$ .
Calculate the matrix product $\mathbf{CA}$ .

The matrices $\mathbf{A}$ , $\mathbf{B}$ and $\mathbf{C}$ are special cases of the general form

$\mathbf{D} = \left(\begin{array}{rr} {\alpha} & {\beta} \\ -{\beta} & {\alpha} \end{array}\right)$ where $\alpha$ and $\beta$ are scalar constants (real numbers).

Find the values of $\alpha$ and $\beta$ , that ensure that $\mathbf{D}$ satisfies the equation $\mathbf{D}^2 = \mathbf{I}$ , where $\mathbf{I}$ is the identity matrix.

A simple model to forecast the weather is based on the probability for rain or sunshine tomorrow, given knowledge of the weather today. Assume that if it rains today there is a 70% probability of rain tomorrow, and if today is sunny there is a 60% probability of sunshine tomorrow.

Construct a matrix $\mathbf{P}$ where the first column indicates rain today and the second culumn indicates sunhine today. The first row indicates rain tomorrow and the second row indicates sunshine tomorrow. A matrix element in $\mathbf{P}$ is the probability that the weather tomorrow corresponds to the row, assuming that the weather today is given by the column.
$\textbf{P}= \begin{array}{rc} & \begin{array}{c}\text{rain today}\phantom{x}\text{sun today}\end{array} \\ \begin{array}{r}\text{rain tomorrow}\\\text{sun tomorrow}\end{array}\hspace{-1em} & \begin{pmatrix}\quad p_{11}\quad&\quad p_{12}\quad\\p_{21}&p_{22}\end{pmatrix} & \end{array}$ Write the probabilities as a fraction or in decimal, but not in percent. A probability of 50% should be written as 1/2 or 0.5.
You can assume that the weather on a given day can be classified as either sunshine or rain. The probabilities for these two outcomes on a given day must therefore sum to 1, irrespective of whether the weather on the day before was sunny or rainy.

Construct $\mathbf{P}$ .

Your answer: It is a which is with entries with dimensions x given by

Correct! Wrong.
The weather today can be described as a column vector, $\mathbf{w}$ , which is one of:
$\text{rain:}\, \begin{pmatrix}1\\ 0\end{pmatrix} \quad \text{sunshine:}\, \begin{pmatrix}0\\ 1\end{pmatrix}.$ Explain why $\mathbf{Pw}$ can be interpreted as a vector indicating the probability of the weather tomorrow.

Calculate $\mathbf{Pw}$ , assuming today is a rainy day.

Your answer: It is a which is with entries with dimensions x given by

Correct! Wrong.
Which expression results in a column vector where the elements are the probabilities of rain and sunshine, respectively, the day after tomorrow, when $\mathbf{w}$ is the vector indicating observed the weather today?
Choose among the following options:
$\mathbf{w'Pw}$
$\mathbf{Pw^2}$
$\mathbf{PwP}$
$\mathbf{P^2w}$
Use matrix multiplication to calculate the vector expressing the probability of the weather the day after tomorrow, assuming that it rains today. The calculation may be easier if you write the matrix elements as fractions, i.e., write, e.g., $\frac{5}{10}$ instead of 0.5.

Calculate the matrix product identified above, assuming rain today.

Your answer: It is a which is with entries with dimensions x given by

Correct! Wrong.
What is the probability of sunshine the day after tomorrow, assuming that it is raining today?

Use a fraction or decimal number in your answer.

Your answer: It is a which is with entries with dimensions x given by

Correct! Wrong.

A Danish company transports products and materials back and forth between a factory in Denmark and a factory in Southern Europe. The goods must be quality checked somewhere in Germany as part of the transit between Denmark and Southern Europe.

The factory in Denmark can be placed either in Vejle og in Esbjerg. The goods must be quality controlled in either Hamburg, Frankfurt or Berlin. The factory in Southern Europe can be placed either in Bilbao, Toulouse, Milan or Porto.

The company wants to place the factories in such a way that the number of usable freight train connections between the cities is as high as possible (given a stop in one the German cities).

The number of train connections between the Danish cities and the German cities is represented by the $2 \times 3$ matrix $\textbf{A}$ , given by:

$\textbf{A}= \begin{array}{rc} & \begin{array}{c}\text{Berlin}\phantom{x}\text{Frankfurt}\phantom{x}\text{Hamburg} \end{array} \\ \begin{array}{r} \text{Esbjerg} \\ \text{Vejle} \end{array}\hspace{-1em} & \begin{pmatrix} \phantom{Be}0\phantom{lin} & \phantom{Fr}2\phantom{urt} & \phantom{Ha}1\phantom{org} \\ \phantom{Be}3\phantom{lin} & \phantom{Fr}3\phantom{urt} & \phantom{Ha}1\phantom{org} \end{pmatrix} & \end{array}$

For example there are $2$ train connections between Esbjerg and Frankfurt, but none between Esbjerg and Berlin.

In a similar way the $3 \times 4$ matrix $\textbf{B}$ represents the train connections between the German and Southern European cities:

$\textbf{B}= \begin{array}{rc} & \begin{array}{c}\text{Bilbao}\phantom{x}\text{Milan}\phantom{x}\text{Porto}\phantom{x}\text{Toulouse} \end{array} \\ \begin{array}{r} \text{Berlin} \\ \text{Frankfurt} \\ \text{Hamburg} \end{array}\hspace{-1em} & \begin{pmatrix} \phantom{Bi}2 & \phantom{Mil}3\phantom{no} & \phantom{P}0\phantom{to} & \phantom{T}1\phantom{use} \\ \phantom{Bl}4 & \phantom{Mil}1\phantom{no} & \phantom{P}2\phantom{to} & \phantom{T}3\phantom{use} \\ \phantom{Bi}0 & \phantom{Mil}2\phantom{no} & \phantom{P}1\phantom{to} & \phantom{T}2\phantom{use} \\ \end{pmatrix} & \end{array}$

The total number of possible train connections between the Danish and Southern European cities are now given by the elements of the matrix $\textbf{C}=\textbf{AB}$ . $\textbf{C}$ is a $2 \times 4$ matrix given by:

$\textbf{C}= \begin{array}{rc} & \begin{array}{c}\text{Bilbao}\phantom{x}\text{Milan}\phantom{x}\text{Porto}\phantom{x}\text{Toulouse} \end{array} \\ \begin{array}{r} \text{Esbjerg} \\ \text{Vejle} \end{array}\hspace{-1em} & \begin{pmatrix} \phantom{Bi}\phantom{a} & \phantom{Mil}\phantom{a}\phantom{no} & \phantom{P}5\phantom{to} & \phantom{T}\phantom{a}\phantom{use} \\ \phantom{Bl}\phantom{a} & \phantom{Mi}14\phantom{no} & \phantom{P}\phantom{a}\phantom{to} & \phantom{T}\phantom{a}\phantom{use} \\ \end{pmatrix} & \end{array}$

For example, there are 5 ways to transport goods between Esbjerg and Porto.

Insert the missing matrix elements in $\textbf{C}$
Where does the company place its two factories?

The company gets news of rumors that the mayors of Frankfurt and Milan are planning more freight trains between their respective cities, and realise that the optimal placement of the two factories may now be Vejle and Milan.

What is the minimum number of train connections between Frankfurt and Milan that makes Vejle and Milan the optimal locations for the two factories?

Show that $\begin{pmatrix} 3 & \phantom{-}0 \\ 2 & -1 \end{pmatrix}^{-1} = \begin{pmatrix} 1/3 & \phantom{-}0 \\ 2/3 & -1 \end{pmatrix}$

Let $\mathbf{B} = \begin{pmatrix} 4 & 7 \\ 3 & 5 \end{pmatrix}$ . Find $\mathbf{A}$ so that $\mathbf{AB} = \mathbf{BA} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$ .

Your answer: It is a

Find the inverse of the matrix, if it exists: $\begin{pmatrix} 9 & 6 \\ 3 & 5 \end{pmatrix}$

Find the inverse of the matrix, if it exists: $\begin{pmatrix} 4 & -4 \\ 2 & -2 \end{pmatrix}$

Solve the linear system by using the inverse matrix:

$\begin{aligned} 2x - 3y & = 3 \\ 3x - 4y & = 5 \end{aligned}$

Solve the linear system by using the inverse matrix:

$\begin{aligned} 4x_1 + 5x_2 & = 9 \\ 4x_1 + 8x_2 & = 24 \end{aligned}$

(Previous exam problem)

Consider the following system of equations:

$\begin{aligned} 3x_1 - x_2 - x_3 & = 5 \\ 2x_1 +x_2 - 2x_3 & = 0 \\ x_1 + 3x_2 + x_3 & = 1 \end{aligned}$

Determine A, x, and b, so that the system of equations can be written in matrix form as:
$\textbf{Ax}= \textbf{b}$ (Note that you have answered this sub-problem in exercise 14.8).
Compute CA and AD, where $\textbf{C} = \begin{pmatrix} \phantom{-}7 & -2 & 3 \\ -4 & \phantom{-}4 & 4 \\ \phantom{-}5 & -10 & 5 \end{pmatrix}$ and $\textbf{D} = \begin{pmatrix} \phantom{-}5 & 24 & 28 \\ 20 & 12 & 24 \\ -5 & 20 & 0 \end{pmatrix}$
(Note that you have answered this sub-problem in exercise 14.8).
Find the scalar $\alpha$ so that $\alpha\textbf{C} = \textbf{A}^{-1}$ (Hint: use that $\textbf{A}^{-1}\textbf{A} = \textbf{I}$ ).
Find the vector x that is a solution to the matrix equation $\textbf{Ax}=\textbf{b}$

(Previous exam problem)

A vector $\mathbf{v}$ and two matrices $\mathbf{U}$ and $\mathbf{W}$ are given by

$\mathbf{U} = \begin{pmatrix} 1 & \sqrt{2} \\ \sqrt{2} & 1 \end{pmatrix}, \qquad \mathbf{v} = \begin{pmatrix} x \\ y \end{pmatrix}, \qquad \mathbf{W} = \begin{pmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{pmatrix},$ where the elements in $\mathbf{v}$ are real variables and the elements in $\mathbf{W}$ are real constants.

Find the inverse matrix of $\mathbf{U}$ .
Calculate $\mathbf{v'Wv}$ , where $\mathbf{v'}$ is the transpose of $\mathbf{v}$ .
Assume that $\mathbf{W}$ is symmetric and determine $\mathbf{W}$ (i.e. all elements in $\mathbf{W}$ ), so that
$\mathbf{v'Wv} = (x - y)^2.$