7Week 42

7.1 Readings for this week's lectures

Sections 14.7-14.8 and 17.2-17.3 in the textbook.

7.2 Readings for this week's exercises

Sections 15.3 and 17.1 in the textbook.

7.3 Notes

Slope of a level curve

If $F(x,y)=c$ and $F_2'(x,y) \neq 0$ , one has

$y' = - \frac{F_1'(x,y)}{F_2'(x,y)}$

Theorem 17.1.1

A differentiable function $z=f(x,y)$ can have a maximum or minimum at an interior point $(x_0, y_0)$ of its domain only if it is a critical point in the sense that the pair $(x,y)=(x_0,y_0)$ satisfies the following two first-order conditions (FOCs):

$f_1'(x,y) = 0$

$f_2'(x,y) = 0$

7.4 Problems

Use the general chain rule for differentiation of composite functions to find $\frac{\partial w}{\partial t}$ and $\frac{\partial w}{\partial s}$ for:

$w=2xy^{2}z^{2}+yz$ where $x=t^{2},y=s$ and $z=t-s$

Let a function of two variables, where $y$ is implicitly a function of $x$ , be given as:

$6x^{3}-8y^{2}+2xy=0$ Find $\frac{dy}{dx}$ by using the formula in the notes.

Let a function of two variables be given as:

$F(x,y)=4xe^{3y}-5x^{2}y^{3}$ Use the formula $\frac{dy}{dx}=-\frac{F_{1}^{\prime}(x,y)}{F_{2}^{\prime}(x,y)}$ in order to find the slope of the level curve for $F(x,y)=4$ in the point $x,y=\left(1,0\right)$ .

The demand $x$ is the quantity of winter jackets that can be sold at price $p$ . For the function:

$x=2p^{3}-4p^{2}+1000$ find the instantaneous change in $p$ w.r.t. $x$ by implicit differentiation, i.e., $\frac{dp}{dx}$

In this exercise, we meet Dorthe. Drag a statement from the boxes at the bottom, so that the sentence is true.

Dorthe lives in Aarhus. That is

for living in Denmark

a necessary condition

a sufficient condition

not a sufficient condition

In this exercise, we meet Dylan. Drag a statement from the boxes at the bottom, so that the sentence is true.

Dylan lives in Denmark. That is

for living in Aarhus

not a necessary condition

a sufficient condition

a necessary condition

Find all critical points of $f\left(x,y\right)$ for:

$f(x,y)=x^{2}-4xy+3y^{2}+6x-8y-8$

Find all the points $\left(x,y\right)$ where $f\left(x,y\right)$ may have a maximum or minimum for the function:

$f(x,y)=-4x^{2}+10xy+3y^{2}+x-y$

(Part of previous exam problem)

The function $f$ is given by:

$f(x, y) = (x-y)^2 -2x -y(3y - 1 -x) + 7$

Find the first and second order derivatives of the function $f$ .
Check whether the function $f$ has an interior stationary point.

Find all the critical points of $f\left(x,y\right)$ for:

$f(x,y)=\frac{1}{3}x^{3}-4y^{3}-3x+12y-1$

Consider the function $h(x,y) = -x^3 + y^3 + 2x - 3y$ .

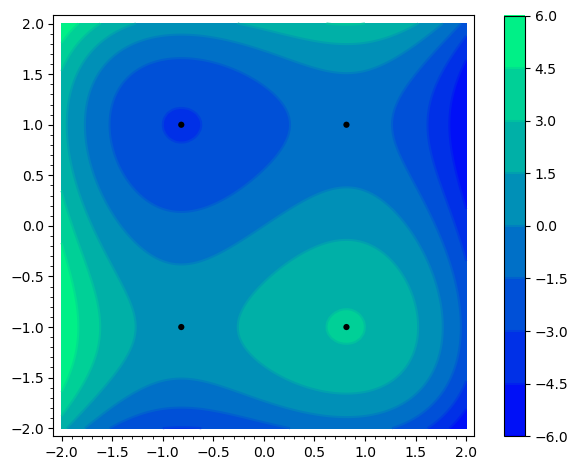
Show that $h$ has the critical points $(x, y) = \left(-\sqrt{2/3} , 1\right),$ $\left(\sqrt{2/3} , 1\right),$ $\left(-\sqrt{2/3} , -1\right),$ $\left(\sqrt{2/3} , -1\right)$
Use the contour plot of $h$ , below, to determine which of these points are a maximum or a minimum.

The postal service provider PostNord requires that any box delivered must have a length plus circumference totaling no more than 300 cm. We call the width $x$ , the height $y$ , and the length $z$ , as shown in the figure below.

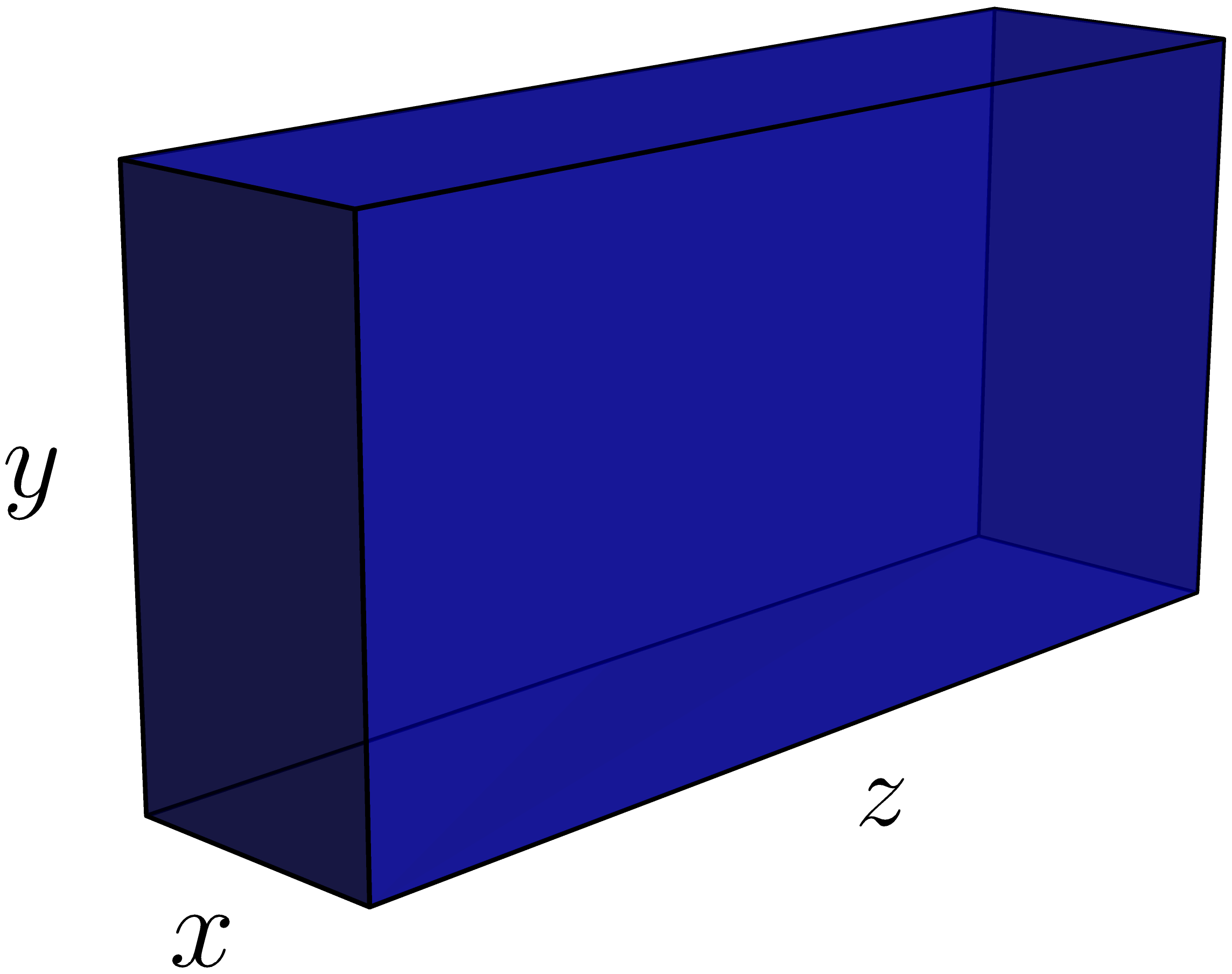
Find the dimensions of the box with the maximum volume that can be sent.

Express the volume, length and circumference in terms of $x$ , $y$ and $z$ as shown in the figure below.

For the maximum volume the following relation holds: $300 \,\mathrm{cm}=$ length + circumference $= z + (2x + 2y)$ . Use this to eliminate $z$ from the expression for $V$ , which can then be written as a function of $x$ and $y$ . Now, find the critical points, which you can assume is a maximum.
PostNord also requires that the maximum length is 150 cm. Does the found solution satisfy this requirement?

Assume that the annual profit of a firm is given by:

$P(x,y) = -2x^2 - 3y^2 + 12x+4y + 10$ where $x$ and $y$ denote the amount of money (in million DKK) spent on product development and advertising, respectively.

Find the firm's profit, when $x=\frac{1}{2}$ and $y=1$ .
Find all possible combinations of $x$ and $y$ , where the profit can be maximized and compute the corresponding profit in these points.