8Week 43

8.1 Readings for this week's lectures

Sections 17.5 and 18.1 in the textbook.

8.2 Readings for this week's exercises

Sections 14.7-14.8 and 17.2-17.3 in the textbook.

8.3 Notes

Necessary conditions for extrema (FOCs)

A differentiable function $z=f(x,y)$ can have an extremum at an interior point $(x_0,y_0)$ of $S$ only if $(x_0,y_0)$ is a critical/stationary point, i.e.,

$f'_1(x_0,y_0) = 0, \qquad f'_2(x_0,y_0) = 0$ Note that these are not sufficient conditions. Stationary points are not necessarily extrema, but all inner extrema are stationary points.

Sufficient conditions for extrema (SOCs)

Let $(x_0,y_0)$ be an interior critical/stationary point for a $C^2$ function $f(x,y)$ defined in a convex set $S$ in $\mathbb{R}^2$ .

If for all $(x,y)\in S$ :

$\frac{\partial^2f}{\partial x^2} \leq 0, \quad \frac{\partial^2f}{\partial y^2} \leq 0, \quad \frac{\partial^2f}{\partial x^2} \frac{\partial^2f}{\partial y^2} - \left( \frac{\partial^2f}{\partial x\partial y} \right)^2 \geq 0,$ then $(x_0,y_0)$ is a maximum for $f$ in $S$ . And a minimum if:

$\frac{\partial^2f}{\partial x^2} \geq 0, \quad \frac{\partial^2f}{\partial y^2} \geq 0, \quad \frac{\partial^2f}{\partial x^2} \frac{\partial^2f}{\partial y^2} - \left( \frac{\partial^2f}{\partial x\partial y} \right)^2 \geq 0$

Sufficient conditions for local extrema (local SOCs)

Let $(x_0,y_0)$ be an interior critical/stationary point for a $C^2$ function $f(x,y)$ defined in a domain $S$ . With

$A=f''_{11}(x_0,y_0),\quad B=f''_{12}(x_0,y_0), \quad C=f''_{22}(x_0,y_0)$

$A<0$ and $AC-B^2>0$ : $(x_0,y_0)$ is a local max
$A>0$ and $AC-B^2>0$ : $(x_0,y_0)$ is a local min
$AC-B^2<0$ : $(x_0,y_0)$ is a saddle point
$AC-B^2=0$ : one of the above

8.4 Problems

Drag the boxes below to the empty slots to construct a true sentence.

The

order conditions are the

conditions and the

order conditions are the

conditions.

first

second

third

sufficient

necessary

both necessary and sufficient

Find all extrema for the function:

$f(x,y) = 2x^2+xy+2y^2+2x+2y+1$ Find the function value(s) of the extrema that you found.

Below is a contour plot plot of a function $g(x,y)$ and set set of points. Answer the folllowing questions and substantiate your answers.

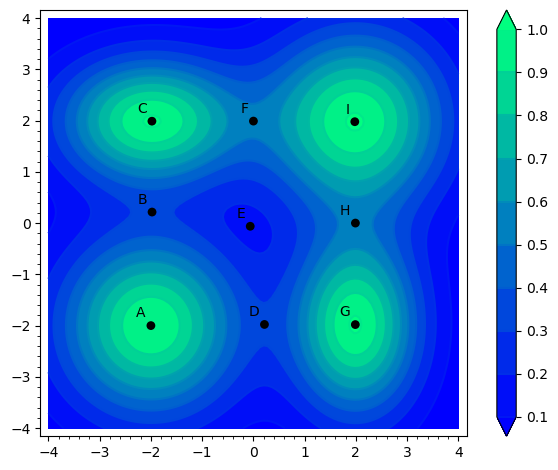
Which of the points are a local maximum?
Which of the points are a localminimum?
Which of the points are a saddlepoint?

Consider the function $h(x,y) = -x^3 + y^3 + 2x - 3y$ .

Insert the correct values of $A$ and $AC-B^2$ and the type of the critical point, for each of the four critical points.

$(x_1, y_1) = (-\sqrt{2/3}, 1),\phantom{-} \quad A =$

, $AC-B^2 =$

Type =

$6\sqrt{2/3}$

$-6\sqrt{2/3}$

$6$

$-6$

$36\sqrt{2/3}$

$-36\sqrt{2/3}$

local min.

local max.

saddle point

$(x_2, y_2) = (\sqrt{2/3}, 1),\phantom{-}\phantom{-} \quad A =$

, $AC-B^2 =$

Type =

$6\sqrt{2/3}$

$-6\sqrt{2/3}$

$6$

$-6$

$36\sqrt{2/3}$

$-36\sqrt{2/3}$

local min.

local max.

saddle point

$(x_3, y_3) = (-\sqrt{2/3}, -1), \quad A =$

, $AC-B^2 =$

Type =

$6\sqrt{2/3}$

$-6\sqrt{2/3}$

$6$

$-6$

$36\sqrt{2/3}$

$-36\sqrt{2/3}$

local min.

local max.

saddle point

$(x_4, y_4) = (\sqrt{2/3}, -1),\phantom{-} \quad A =$

, $AC-B^2 =$

Type =

$6\sqrt{2/3}$

$-6\sqrt{2/3}$

$6$

$-6$

$36\sqrt{2/3}$

$-36\sqrt{2/3}$

local min.

local max.

saddle point

Find all maxima, minima and saddle points of the function $f(x,y)$ (if any), given that we have $f'_1=4x^2-8$ and $f'_2=5y-15$ .

Find all locations and values of local maxima and minima as well as the location of potential saddle points given by the function:

$f(x,y)=x^3+y^3+6x^2-6y^2-2$

Consider the function:

$f(x,y) = \ln(4+2x^2y)$

Define the domain.
Find all local extrema of the function (if any).

Which of the sets below are convex?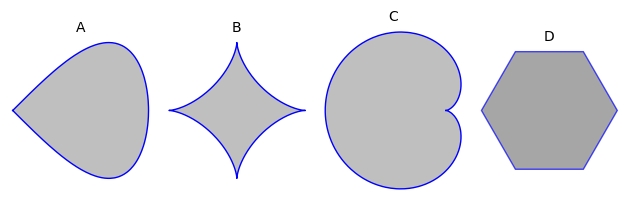

(Previous exam problem)

A function $f(x,y)$ is given by the expression

$f(x,y) = x^2-6x+y^2+4y+xy+8$

Find the critical/stationary point for the function.
Characterise the stationary point using the local second-order conditions, i.e., determine whether the stationary point is a maximum, a minimum, or a saddle point. If it is a maximum or a minimum is it a global extremum?