9Week 44

9.1 Readings for this week's lectures

Sections 18.2–18.5 in the textbook.

9.2 Readings for this week's exercises

Sections 17.5 and 18.1 in the textbook.

9.3 Notes

Recipe for finding extrema (box page 714)

Find all critical/stationary points in $S$ .
Find maxima and minima on the boundary of $S$ .
From these points, the one with the largest function value is the maximum for $f$ in $S$ and the one with the smallest function value is the minimum for $f$ in $S.$

The Lagrange multiplier method

To find a max/min for $f(x,y)$ under the constraint $g(x,y)=c$ ...

Construct ${\cal L} (x,y) = f(x,y) - \lambda \left( g(x,y)-c \right)$
Differentiate ${\cal L}$ wrt $x$ and $y$ and set ${\cal L}'_x = {\cal L}'_y = 0$ .
This gives the three equations:
${\cal L}'_1(x,y) = f'_1(x,y) - \lambda g'_1(x,y) = 0$
${\cal L}'_2(x,y) = f'_2(x,y) - \lambda g'_2(x,y) = 0$
$g(x,y) = c$
Solve these for $(x,y,\lambda)$ . These are the solution candidates.

9.4 Problems

Consider the following three sets:

$\begin{aligned} S_1 & = \{(x,y):5x^2+5y^2 \leq 9\} \\ S_2 & = \{(x,y):5x+8y>8\} \\ S_3 & = \{(x,y):2x+5y\geq8\} \end{aligned}$

Answer the following questions for each of the sets:

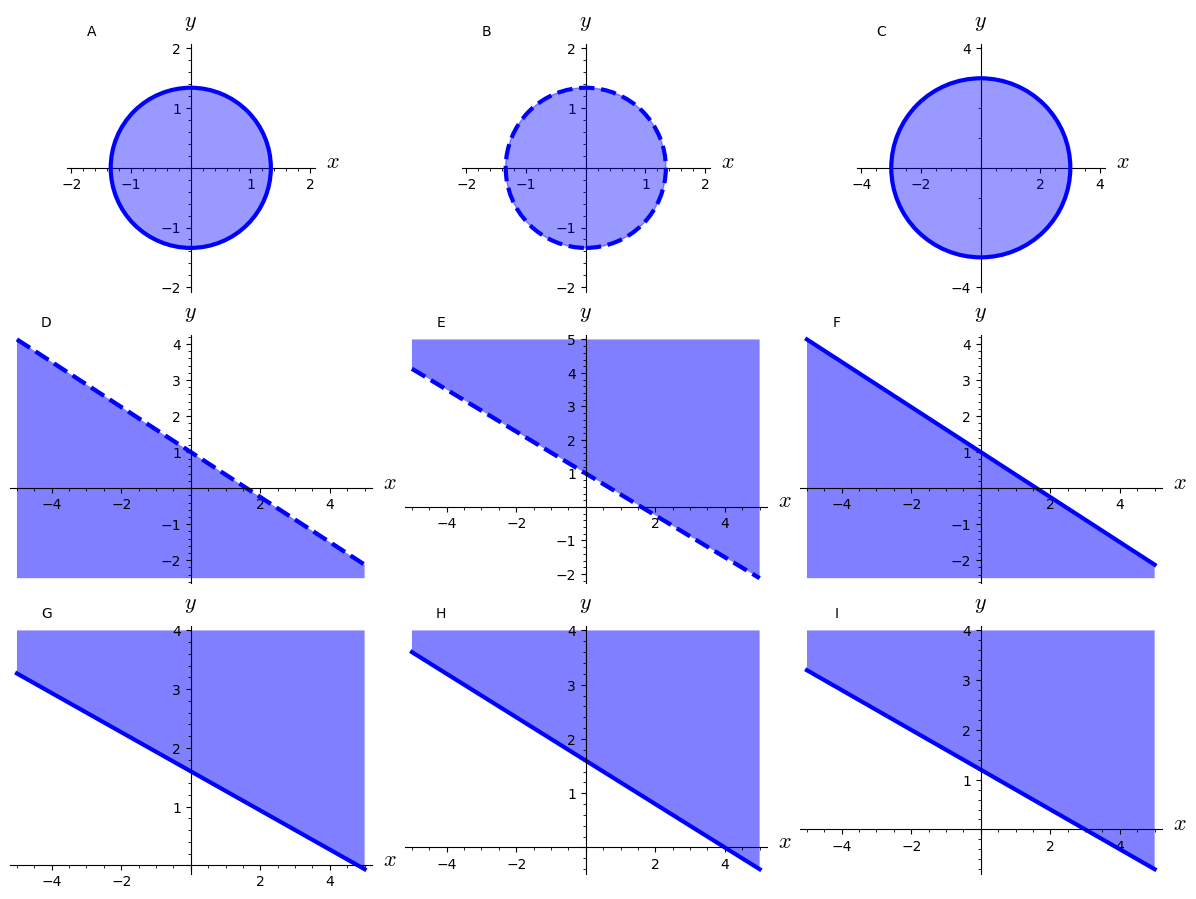
Which of the figures below depicts the set?
Is the set open or closed (or neither or both)?
Is the set bounded?
Is the set compact?

Find the global maximum and minimum of the function on the given domain. The function is given by

$f(x,y) = x^2+5y^2$ in the domain composed of the closed triangular plate bounded by the lines $x=0$ , $y=0$ and $y+2x=2$ in the first quadrant. What are the function values in these points?

Find the maximum and minimum points for the function:

$f(x,y)=x^2 +xy + y^2 -9x + 4$ in the set bounded by the inequalities $0\leq x\leq 7$ and $-4\leq y\leq 0$ .

Use the method of Lagrange multipliers to find the maximum value of $f(x,y)$ subject to the given constraint. We have that:

$f(x,y) = xy$ subject to:

$x+y = 288$

A function $f(x, y)$ has the contour plot shown below in Figure A. Lighter areas correspond to higher function values and darker areas to lower function values.

What are the coordinates for the point that maximises $f(x, y)$ ? Read the coordinates off the figure as well as you can.

Figure B shows a constraint as a blue line.

What are the coordinates for the point that maximises $f(x, y)$ subject to the constraint?

A second constraint is shown in Figure C as the blue curve, along with some points. Answer the questions below by indicating the point(s) consistent with the correct answer.

Where does the function have a maximum subject to the constraint?
Where does the function have a minimum subject to the constraint?

Use the method of Lagrange multipliers to find the maximum value of $f(x,y)$ subject to the given constraint. We have that:

$f(x,y) = 30-x^2-y^2$ subject to:

$x+5y = 26$

A minimisation problem with constraints is given by

$\text{min} \, f(x,y)=2x^2+4y^2,$ with the constraint:

$34-2x-3y=0.$ Solve the minimisation problem.

A student has the utility function $u(x,y)=100xy+x+2y$ . Assume that the price per unit of coffee $x$ is 10 DKK and that the price for a meal (food) $y$ is 20 DKK. The student is able to use 2000 DKK a month on coffee and food.

Solve the utility maximisation problem.

(Previous exam problem)

A constrained minimisation problem is given by

$\min f(x,y) = x^2+y^2$ such that

$x^2y=2000$ Find the solutions(s) to the problem.

Take a look at section 18.3 in the book.