2Uge 37

2.1 Pensum til denne uges forelæsning

Sektion 6.8 – 6.11 og 8.5 i lærebogen.

2.2 Pensum til denne uges opgaver

Sektion 6.1 – 6.7 i lærebogen.

2.3 Noter

Nogle vigtige resultater, som kan være nyttige i forbindelse med denne uges opgaver er gengivet nedenfor.

Regler for grænseværdier

Lad $\displaystyle A = \lim_{x \to a} f(x)$ og $\displaystyle B = \lim_{x \to a} g(x)$ . Så gælder:

$\begin{aligned} \lim_{x \to a} \left( f(x) \pm g(x) \right) &= A \pm B \\ \lim_{x \to a} \left( f(x) g(x) \right) &= AB \\ \lim_{x \to a} \frac{f(x)}{g(x)} &= \frac{A}{B}, \quad \text{hvis~} B \neq 0 \\ \lim_{x \to a} \left( f(x) \right)^r &= A^r \end{aligned}$

Lighed af grænseværdier

Hvis to funktioner $f(x)$ og $g(x)$ opfylder $f(x) = g(x)$ i en omegn af $a$ , men ikke nødvendigvis i $x = a$ , og en af grænseværdierne for $x \to a$ eksisterer, så gælder:

$\lim_{x \to a} f(x) = \lim_{x \to a} g(x)$

Differentialkvotienter af udvalgte funktioner

$\begin{aligned} \underline{f(x)} \qquad {}& \underline{f'(x)} \qquad {}& \underline{\text{Note}}\\ x^a \qquad {}& a x^{a-1} \qquad {}& \\ e^x \qquad {}& e^x \quad {}& \\ \ln(x) \qquad {}& 1/x \quad {}& x > 0 \\ e^{ax} \qquad {}& ae^{ax} \quad {}& \\ a^{x} \qquad {}& \ln(a) a^{x} \quad {}& a > 0 \end{aligned}$

Regneregler for differentialkvotienter

$\begin{aligned} {}&\frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \left( A + f(x) \right) = \frac{\mathrm{d}f}{\mathrm{d}x} = f'(x)\\[3ex] {}&\frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \left( A \cdot f(x) \right) = A \frac{\mathrm{d}f}{\mathrm{d}x} = A f'(x)\\[3ex] {}&\frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \left( f(x) \pm g(x) \right) = \frac{\mathrm{d}f}{\mathrm{d}x} \pm \frac{\mathrm{d}g}{\mathrm{d}x} = f'(x) \pm g'(x)\\[3ex] {}&\frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \left( f(x) g(x) \right) = \frac{\mathrm{d}f}{\mathrm{d}x} g(x) + f(x) \frac{\mathrm{d}g}{\mathrm{d}x} = f'(x)g(x) + f(x)g'(x)\\[3ex] {}&\frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \left( \frac{f(x)}{g(x)}\right) = \frac{\frac{\mathrm{d}f}{\mathrm{d}x} g(x) - f(x) \frac{\mathrm{d}g}{\mathrm{d}x}}{(g(x))^2} = \frac{f'(x)g(x) - f(x)g'(x)}{(g(x))^2} \end{aligned}$

Ligningen for tangenten i et punkt

Ligningen for tangenten til grafen for $f(x)$ i punktet $(x_0, f(x_0))$ er givet ved udtrykket

$y = f(x_0) + f'(x_0) (x - x_0) \tag{2.1}$

2.4 Opgaver

Formålet med denne opgave er at illustrere at tangenten er grænsen for sekanten, når $h \to 0$ .

Definitionen på differentialkvotienten $f'(x_0)$ er nedenstående grænseværdi af Newton-kvotienten

$f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \tag{2.2}$ Men hvad betyder det? Vi kan tolke Newton-kvotienten geometrisk som hældningen på linjen gennem punkterne

$(x_0, f(x_0)) \quad \text{og}\quad (x_0 + h, f(x_0 + h)).$ Denne linje kaldes sekanten. Differentialkvotienten er så grænsen hvor de to punkter kommer infinitesimalt tæt på hinanden, altså grænsen $h \to 0$ .

Lad os kigge på en bestemt funktion, nemlig

$f(x) = -x^3 + 5x^2 + 2.$ Hvis vi ønsker at beregne $f'(2)$ kan vi altså benytte ligning 2.2 med $x_0 = 2$ . I stedet for at beregne grænseværdien, kan vi udforske problemet numerisk, fx med en lommeregner, og beregne sekantens hældning for forskellige værdier af $h$ , som bliver mindre og mindre.

Nedenfor er vist et interaktivt plot, hvor du kan plotte sekanten for forskellige værdier af $h$ . I plottet vises også hældningen af sekanten, altså værdien af Newton-kvotienten. Du ændrer $h$ ved at trække i punktet $x = x_0 + h$ .

Beskriv hvad der sker, når $h$ bliver mindre og mindre
Beregn $f'(x)$ ved brug af regneregler for differentialkvotienter
Beregn værdien $f'(2)$
Sammenlign værdien fra plottet for den mindste værdi af $h$ med den eksakte værdi for $f'(2)$
Plottet er lavet så du ikke kan sætte $h = 0$ Hvorfor? Hvad ville der ske hvis $h=0$ ?

Netop fordi vi ikke blot kan sætte $h = 0$ i Newton-kvotienten har vi brug for at tage grænseværdien. Differentialregning er en smart måde at beregne disse grænseværdier uden at vi hver gang behøver at gå tilbage til ligning 2.2.

I denne opgave ser vi på samme funktion som i opgave 2.1.

Prøv at zoome ind på punktet $(2, f(2))$ . Hvis du kommer tæt nok på er kurven umulig at skelne fra en ret linje. Dette gælder for alle kontinuerte funktioner. Den rette linje du ser når du zoomer nok ind er identisk med tangenten (i grænsen hvor du har zoomet uendeligt).

Du kan zoome i grafen nedenfor ved at markere et område (træk og slip). Du kan zoome helt ud igen ved at dobbelt-klikke på grafen.

a) Find hældningen af kurven i punktet $(3, f(3))$ .

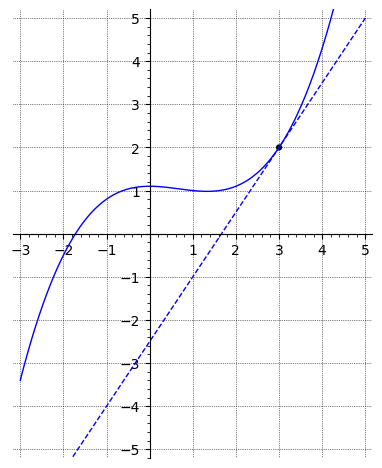
b) Hvor har kurven en hældning på nul?

$x \approx -1.72$

$x = 1.666\ldots$

$x = 0$ og $x = 1.333\ldots$

$x \approx -1.72$ og $x = 1.666\ldots$

En funktion $f(x)$ og dens afledede $f'(x)$ har funktionsværdierne

$\begin{array}{rl} f(-1) &=& 0.65 \\ f'(-1) &=& 0.45 \end{array}$ Hvad er ligningen for tangenten til kurven i punktet $(-1, f(-1))$ , som er vist i figuren nedenfor?

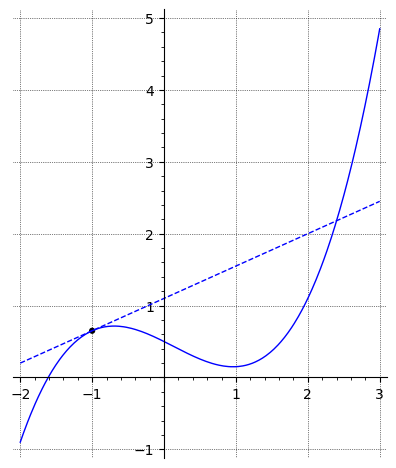
Tangenten til kurven for funktionen $f(x)$ i punktet $(2, f(2))$ er givet ved ligningen

$y = 2.1 x - 3.1$ Hvad er værdierne for $f(2)$ og $f'(2)$ ?

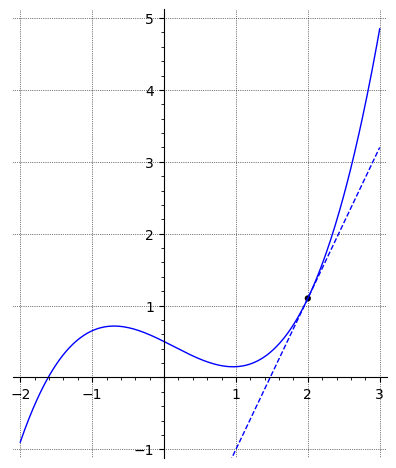
Grafen nedenfor viser kurven for en funktion $f(x)$ .

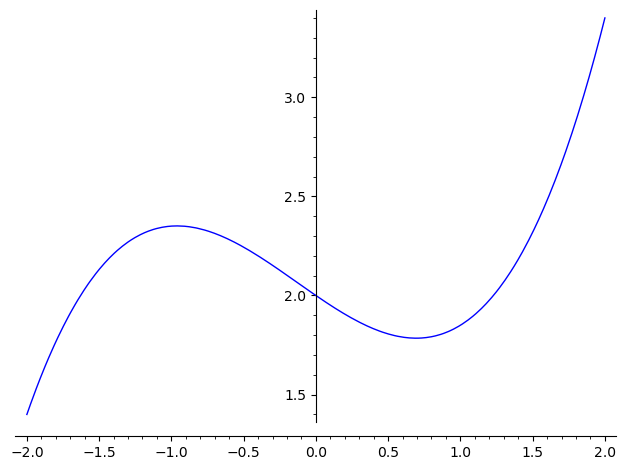
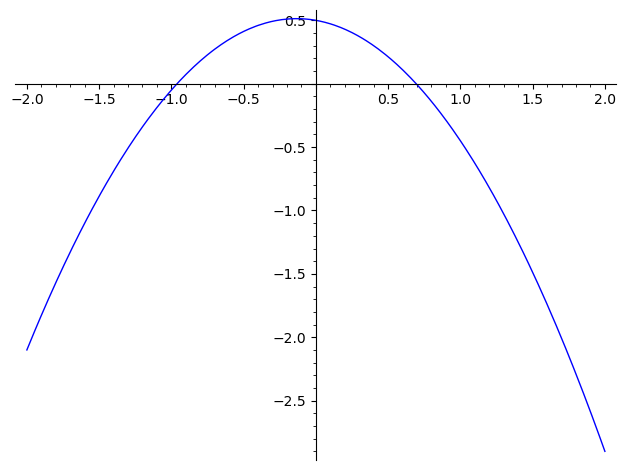
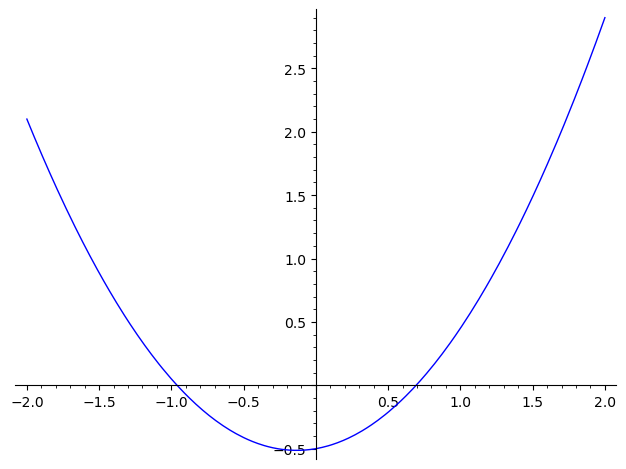
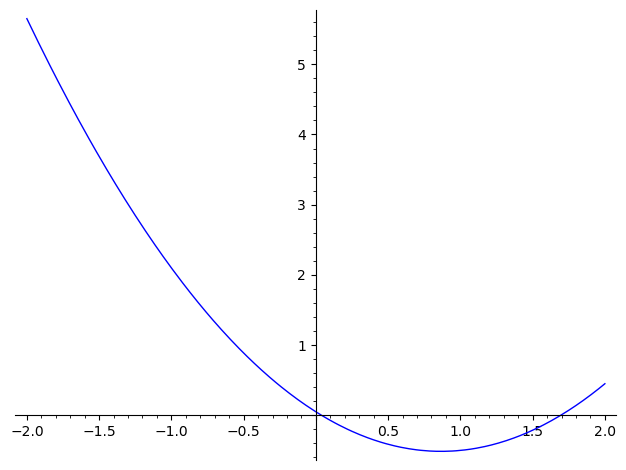
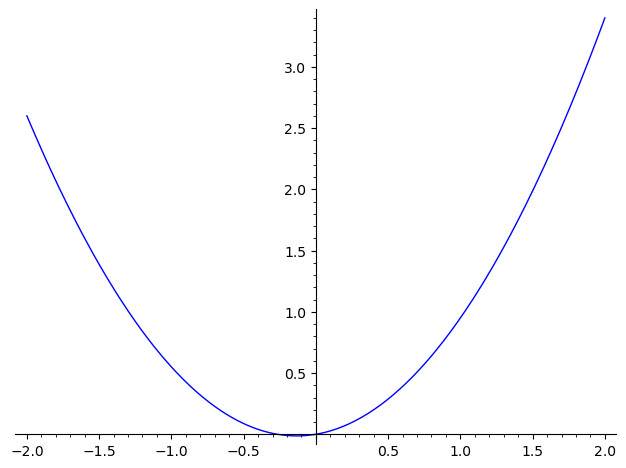
Hvilke(n) af nedenstående grafer viser differentialkvotienten for $f(x)$ ?

Figuren nedenfor viser grafen for en funktion $f(x)$ (blå kurve) og dens afledede $f'(x)$ (stiplet rød kurve).

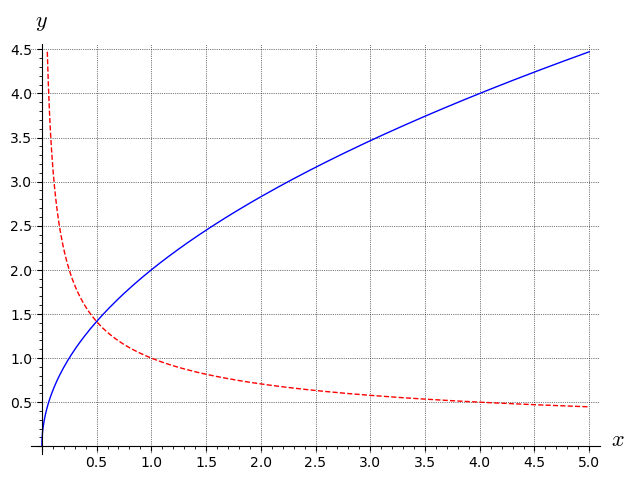Find ligningen for tangenten til $f(x)$ for $x = 4$ .

Hvad er værdierne af $f(4)$ og $f'(4)$ ?

Benyt ligning 2.1.

Find nedenstående grænseværdier

$\displaystyle \lim_{x \to -3} \left( x^2 + 4x + 2 \right)$
$\displaystyle \lim_{x \to 3/2} \left( (x - \frac{2}{3}) (x + \frac{1}{2}) \right)$
$\displaystyle \lim_{x \to 0} \left( \sqrt{(2-x)(8+x)} + \frac{1}{x-2} \right)$
$\displaystyle \lim_{x \to 3} \frac{2x^2-2x-2}{x+2}$

Beregn grænseværdien

$\lim_{x \to 2} \frac{3x^2 - 3x - 6}{2x^2 + 2x - 12}$

Er du sikker på at du ikke vil prøve selv, først? Brug hints med omtanke!

Ja, vis mig et hint, jeg sidder fast!

Benyt resultatet lighed af grænseværdier ovenfor. Tænk over hvordan du kan omskrive tæller og nævner.

Omskriv tæller og nævner ved at faktorisere (se formel (1.5) i boksen Andengradsligning i afsnit 1.3.1).

Differentiér følgende funktioner

$f(x) = 3x^6$
$g(x) = x^{3/2}$
$h(y) = \frac{2}{3} y^{-3}$
$q(x) = 1 / (x^{-7/3})$
$p(x) = \displaystyle\frac{\sqrt[4]{x}}{7}$

Udregn differentialkvotienterne af følgende funktioner

$f(x) = 2ax^3$ , hvor $a$ er en konstant.
$f(z) = 2\sqrt{z} - \frac{1}{7}z^5$ .
$f(x) = ax^2 + bx + c$ , hvor $a$ , $b$ og $c$ er konstanter.
$g(y) = 5y^3 - 3y^2$ .

Beregn $y'(x)$ når $y$ er givet ved:

$y = 5x^2 - 3x + 7$
$y = x^7 + 3 \sqrt{x} + \frac{1}{2 \sqrt{x}}$
$y = x \cdot (x -2x^{-1})$

Beregn den afledede af følgende funktioner:

Her skal produktreglen bruges. Det kan tit være en god idé at starte med at skrive op hvad de fire størrelser, $f(x), g(x), f'(x)$ og $g'(x)$ der indgår i reglen, og beregne de afledede. F.eks. i opgave 1 nedenunder er det oplagt at se $10x^3$ som den første funktion og $1-\sqrt{x}$ som den anden funktion. De afledede er hhv. $30x^2$ og $-\frac{1}{2 \sqrt{x}}$ .

$f(x) = 10x^3 (1 - \sqrt{x})$
$g(x) = (2x - x^2)(x^3 + x^2) + 1000$
$h(x) = (x + 2)\cdot (\sqrt{x} -3x)$

Beregn differentialkvotienten mht. $x$ af nedenstående udtryk:

Se video for eksempel her

$\displaystyle \frac{\sqrt{x} - 1}{x^2}$
$\displaystyle \frac{x-2}{x+2}$
$\displaystyle \frac{2x-3}{5x+4}$