5Uge 40

5.1 Pensum til denne uges forelæsning

Sektion 15.1-15.2 i lærebogen.

5.2 Pensum til denne uges opgaver

Sektion 14.2-14.3 og 14.6 i lærebogen.

5.3 Noter

Partiel differentiation

Hvis $z=f(x,y)$ , så er

$\frac{\partial z}{\partial x} = f'_x(x,y) = f'_1(x,y) = \text{den partielle afledte af~} f(x,y) \text{~med hensyn til~} x.$

$\frac{\partial z}{\partial y} = f'_y(x,y)=f'_2(x,y) = \text{den partielle afledte af~} f(x,y) \text{~med hensyn til~} y.$ For at differentiere partielt med hensyn til en variabel, opfat den anden variabel som en konstant. Vi kan således midlertidigt opfatte $f$ som en funktion af kun en variabel. Eksempel: For at finde $\frac{\partial z}{\partial x}$ , tænk på $y$ som en konstant, og differentiér $f(x,y)$ som om $f$ kun afhang af $x$ .

5.4 Opgaver

Træk udtrykkene i de nederste kasser op i de tomme kasser, så ligningerne kommer til at passe.

$f'_x(x,y) =$

$\frac{\partial z}{\partial y} =$

$f''_{xy}(x,y) =$

$f''_{yy}(x,y) =$

$\frac{\partial^2 f}{\partial x\partial y}$

$\frac{\partial^2 f}{\partial^2 y}$

$\frac{\partial f}{\partial x}$

$z'_y(x, y)$

$\frac{\partial^2 f}{\partial y^2}$

$\frac{\partial^2 f}{\partial y\partial x}$

$z'_1(x, y)$

En funktion $z = f(x,y)$ er defineret som:

$z=f(x,y) = 3x^5 + 4y^2-8xy$ Find:

$\frac{\partial z}{\partial x}$
$\frac{\partial z}{\partial y}$
$f'_1(-1,1)$
$f'_2(-1,-1)$

En funktion $z = f(x,y)$ er defineret som:

$f(x,y) = \sqrt{x^2+y^2}$ Find:

$f'_1$
$f'_2$
$f'_1(-2,-8)$
$f'_2(3,7)$

For funktionen $f(x,y)=e^{8xy}$ , find $f'_x$ og $f'_y$ .

Betragt en produktionsfunktion $Y=F(K,L)$ , hvor $K$ er enheder kapital og $L$ er enheder arbejdskraft. $Y$ betegner antal producerede enheder.

Forbind udsagnene nedenfor med de korrekte matematiske udtryk ved at trække de matematiske udtryk op i de kasser der passer til udsagnene.

a) Med 10 enheder kapital og 25 enheder arbejdskraft kan der produceres 5 enheder

b) Ved 10 enheder kapital og 25 enheder arbejdskraft vil en lille stigning i enheder arbejdskraft cirka give 2 ekstra producerede enheder per ekstra enhed af arbejdskraft

c) Jo flere enheder arbejdskraft, jo større er effekten af en ekstra enhed kapital på produktionen

$F_K'(10,25)=5$

$F(10,25) = 5$

$F_{KL}''(K,L)<0$

$F_K'(10,25)=2$

$F_K'(K,10) > F_K'(K,15)$

$F(25,10)=5$

$F_{KL}''(K,L) > 0$

$F_L'(10,25)=2$

For funktionen $f(x,y)=x\ln(4x+y)$ , find $f'_x$ og $f'_y$ .

Find $\frac{\partial z}{\partial y}$ hvis $z = 2(8x+4y)^3$

Find koordinaterne til punkterne A, B og C i boksen som er vist nedenfor.

Figuren nedenunder viser tre niveaukurver for en funktion $z=f(x,y)$ . For hver niveaukurve angives værdien af $z$ lige over den pågældende kurve.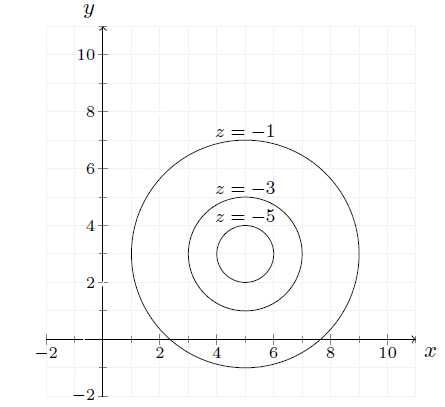

Bestem $f(1,3), f(6,3), f(5,5)$ og $f(5,-1)$
Løs ligningerne $f(4,y)=-5$ og $f(x,3)=-1$
Find approksimationer for $f_x'(6,3)$ og $f'_y(5,4)$

En funktion har nedenstående konturplot, hvor springet mellem niveaukurverne er konstant.

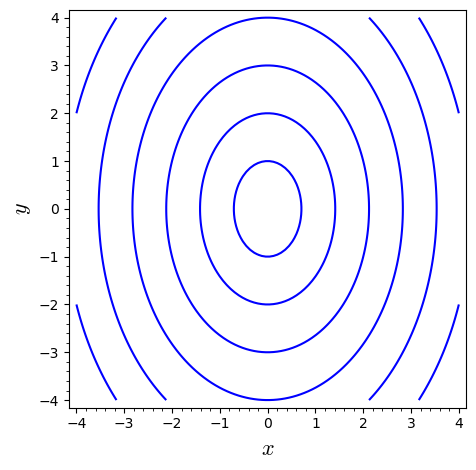
Hvilken af følgende funktioner er vist i konturplottet? Forklar hvordan du kommer frem til svaret.

Brug udelukkelsesmetoden og overvej svaret på følgende to spørgsmål:

Hvad betyder det at niveaukurverne har samme afstand langs en given linje gennem $(0, 0)$ , fx $x$ -aksen eller $y$ -aksen?
I hvilken retning vokser funktionen hurtigst? Det kan du se ved at kigge på afstanden mellem niveaukurverne.

$x^2 + 2y^2$

$\sqrt{x^2 + 2y^2}$

$2x^2 + y^2$

$\sqrt{2x^2 + y^2}$

Nedenfor er vist en række konturplot. Match hvert enkelt plot med den funktion plottet repræsenterer. De blå linjer viser niveaukurverne for 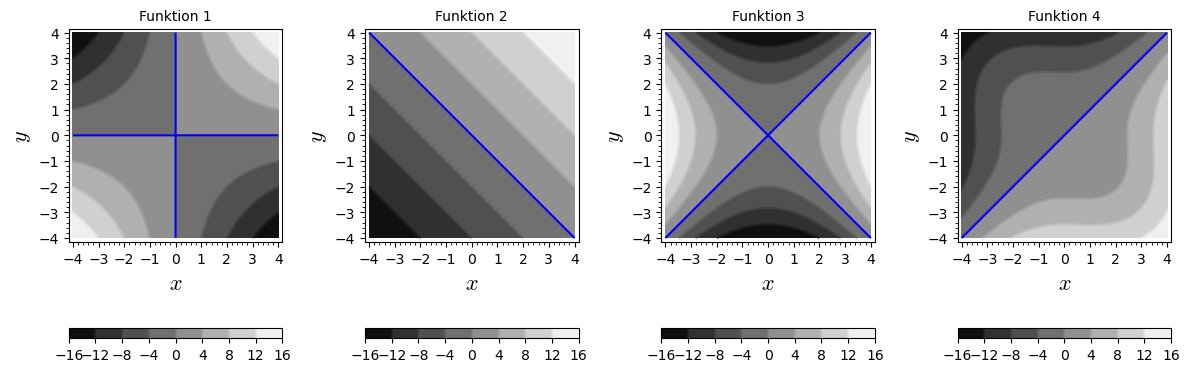$z = 0$ .

Se fx på løsningen til $f(x, y) = 0$ som svarer til de blå kurver i plottene.

Funktion 1:

Funktion 2:

Funktion 3:

Funktion 4:

$2(x^3 - y^3) \Big/ 3\sqrt{x^2 + y^2}$

$xy$

$x^2 - y^2$

$2(x+y)$

Betragt funktionen:

$z=\frac{1}{3}\left ( x^2+y^2 \right )$ Tegn niveaukurverne for $z=c$ hvor $c=0,1,2,3,4$ .

Bestem niveaukurven for funktionen $f(x,y) = \sqrt{30-x^2-y^2}$ til værdien $c=5$ og tegn kurven.

For funktionen $f(x,y,z)=8+2xy^4-5z^5$ , find $f'_1$ , $f'_2$ og $f'_3$ .

Lad

$f(x,y,z)=\frac{9+x^2y^4}{z^3}$ Find $\frac{\partial f}{\partial x}$ , $\frac{\partial f}{\partial y}$ , og $\frac{\partial f}{\partial z}$

Denne opgave viser et eksempel hvor Youngs teorem ikke holder. Denne opgave er frivillig, for de særligt interesserede.

Betragt funktionen $h(x, y) = \frac{{\left(x^{2} - y^{2}\right)} x y}{x^{2} + y^{2}}$ , som er plottet nedenfor.

Det eneste problem med $h(x)$ er at den ikke er defineret i $(x, y) = (0, 0)$ . Men grænserne for $x\to 0$ og $y\to 0$ eksisterer:

$\begin{aligned} \lim_{x\to 0} h(x, 0) &= 0 \\ \lim_{y\to 0} h(0, y) &= 0 \end{aligned}$

Vi kan derfor definere en funktion, som er kontinuert for alle $(x, y)$ inklusiv $(0, 0)$ som følger:

$f(x,\,y) = \begin{cases}{\frac {xy\left(x^{2}-y^{2}\right)}{x^{2}+y^{2}}}&{\text{ for }}(x,\,y)\neq (0,\,0),\\0&{\text{ for }}(x,\,y)=(0,\,0).\end{cases}$

Det er ikke svært at beregne de partielle afledede af $f(x, y)$ , men det er ret omstændeligt, så her er resultatet, som du kan eftervise, hvis du har lyst:

$\begin{aligned} f'_x(x, y) &= \frac{2 \, x^{2} y}{x^{2} + y^{2}} - \frac{2 \, {\left(x^{2} - y^{2}\right)} x^{2} y}{{\left(x^{2} + y^{2}\right)}^{2}} + \frac{{\left(x^{2} - y^{2}\right)} y}{x^{2} + y^{2}} \\ f'_y(x, y) &= -\frac{2 \, x y^{2}}{x^{2} + y^{2}} - \frac{2 \, {\left(x^{2} - y^{2}\right)} x y^{2}}{{\left(x^{2} + y^{2}\right)}^{2}} + \frac{{\left(x^{2} - y^{2}\right)} x}{x^{2} + y^{2}} \end{aligned}$

Vis at $f'_x(0, y) = -y$
Vis at $f'_y(x, 0) = x$

Nu kan vi beregne de afledte af anden orden i punktet $(0, 0)$ som:

$\begin{aligned} f''_{xy}(0, 0) &= \frac{\partial f'_x(0, y)}{\partial y} (0, 0)\\ f''_{yx}(0, 0) &= \frac{\partial f'_y(x, 0)}{\partial x} (0, 0) \end{aligned}$

Beregn $f''_{xy}(0, 0)$ og $f''_{yx}(0, 0)$ som vist ovenfor.
Hvad er konklusionen?