8Uge 43
8.1 Pensum til denne uges forelæsning
Afsnit 17.5 og 18.1 i lærebogen.8.2 Pensum til denne uges opgaver
Afsnit 14.7-14.8 og 17.2-17.3 i lærebogen.8.3 Noter
Nødvendige betingelser for ekstrema (FOCs)
En differentiabel funktion kan kun have et ekstremum i et indre punkt i en mængde ,
hvis er et kritisk/stationært punkt, dvs.
Bemærk at dette ikke er en tilstrækkelig betingelse. At den er opfyldt betyder ikke, at et punkt er et
ekstremum. Men alle indre ekstrema er kritiske punkter.
Tilstrækkelige betingelser for ekstrema (SOCs)
Lad være et indre kritisk/stationært punkt for en funktion defineret i en konveks mængde . Hvis der for alle gælder:
så er et maximum for i , og et minimum hvis:
Tilstrækkelige betingelser for lokale ekstrema (lokale SOCs)
Lad være et indre kritisk/stationært punkt for en funktion defineret i mængden . Med :
- og : er lokalt max
- og : er lokalt min
- : er saddelpunkt
- : én af ovenstående
8.4 Opgaver
Træk ordene i de nederste kasser op i de tomme kasser, så sætningen bliver korrekt. betingelserne er betingelser og betingelserne er betingelser.
førsteordens
andenordens
tredjeordens
de tilstrækkelige
de nødvendige
både de nødvendige og de tilstrækkelige
Find alle ekstrema for funktionen:
Find funktionsværdien for de fundne ekstrema.
Nedenfor er vist et konturplot af en funktion samt en række punkter. Besvar følgende spørgsmål, og begrund dine svar.
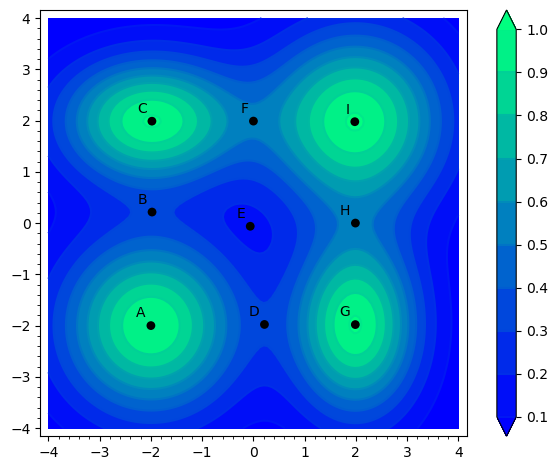
- Hvilke af de viste punkter er et lokalt maksimum?
- Hvilke af de viste punkter er et lokalt minimum?
- Hvilke af de viste punkter er saddelpunkter?

Betragt funktionen .Indsæt de korrekte værdier af og og typen af det kritiske punkt, for hvert af de fire kritiske punkter.
, Type =
lokalt min.
lokalt max.
saddelpunkt
, Type =
lokalt min.
lokalt max.
saddelpunkt
, Type =
lokalt min.
lokalt max.
saddelpunkt
, Type =
lokalt min.
lokalt max.
saddelpunkt
Find maksima, minima og saddelpunkter af funktionen (hvis nogen overhovedet), givet at og .
Find alle lokationer og værdier af lokale maksima og minima samt lokationen til potentielle saddelpunkter i forhold til følgende funktion:
Betragt den følgende funktion:
- Bestem definitionsmængden.
- Find alle lokale extrema til funktionen (hvis nogen).
Hvilke af nedenstående mængder er konvekse?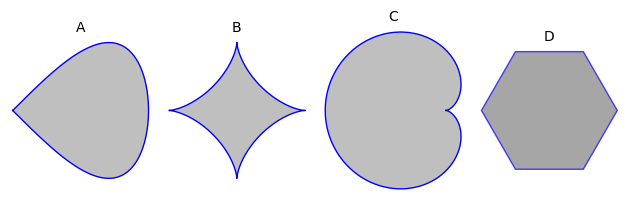

(Tidligere eksamensopgave)
En funktion er defineret som
- Find det kritiske/stationære punkt for funktionen.
- Karakterisér det kritiske punkt vha. de lokale andenordensbetingelser, dvs. find ud af hvorvidt det kritiske punkt er et lokalt maksimum, et lokalt minimum eller et saddelpunkt. Hvis det er et lokalt maksimum eller et lokalt minimum, er det da et globalt ekstremum?