4Uge 39
4.1 Pensum til denne uges forelæsning
Sektion 14.2-14.3 og 14.6 i lærebogen.4.2 Pensum til denne uges opgaver
Sektion 7.3, 7.12 og 14.1 i lærebogen.4.3 Noter
Differentiation af invers funktion
Hvis er den inverse funktion til , gælder der
L'Hôpitals regel
Hvis og ,
og , så gælder l'Hôpitals regel:
Selv hvis og ikke er definerede i kan den generelle udgave af
l'Hôpitals regel anvendes:
Gælder også hvis grænseværdien er
4.4 Opgaver
Lad en funktion være givet ved udtrykket for .
Find differentialkvotienten for den inverse funktion, i punktet
.
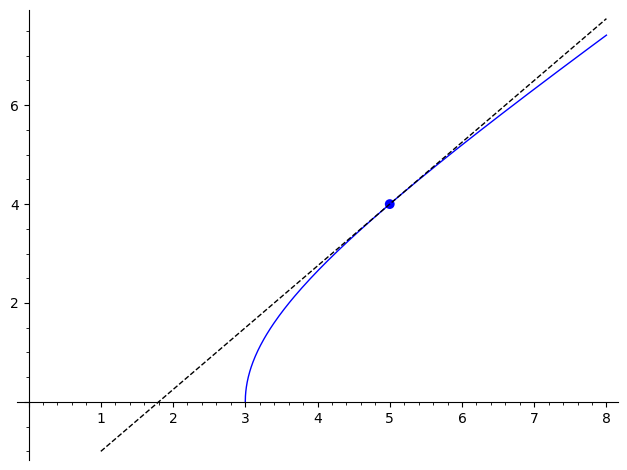
En funktion har grafen vist nedenfor. I punktet har funktionen
en tangent beskrevet af ligningen . Antag at den inverse funktion
til er . Find værdien af differentialkvotienten for den inverse funktion for .

Besvar nedenstående, hvor .
- Beregn værdien af for ud fra .
- Find et eksplicit udtryk for den inverse funktion .
- Find et udtryk for og beregn .
- Har du fået samme resultat i pkt. 1 og 3?
Beregn nedenstående grænseværdier.
Kan l'Hôpitals regel anvendes til at beregne nedenstående grænseværdi?
Hvis, ja, find grænseværdien.
Beregn grænseværdien
Bemærk at du har set denne grænseværdi før i opgave 2.9.
I denne opgave kigger vi på sandsynligheden for at to personer i en gruppe af mennesker har fødselsdag samme dag. Vi er interesseret i hvordan denne sandsynlighed udvikler sig som antallet af personer, , i gruppen vokser.Under antagelse af at der er 365 dage på et år og at alle fødselsdage er lige sandsynlige, kan sandsynligheden for to fødselarer på samme dag, , beskrives somFunktionen er plottet nedenunder.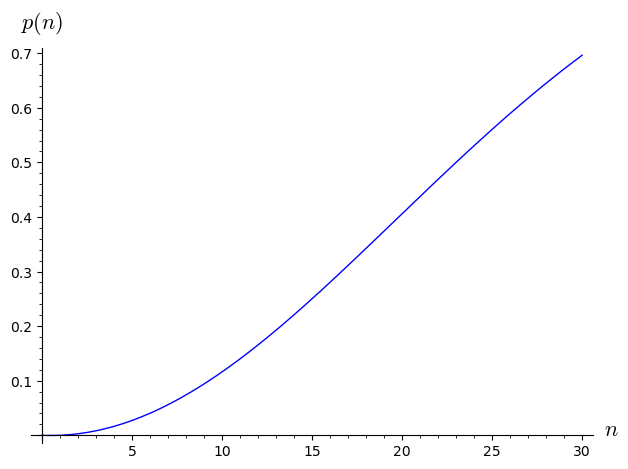

Vis at mængden af dej til en cylinderformet pizzabund med radius og tykkelse , som vist nedenfor,
kan skrives som nedenstående funktion af to variable.
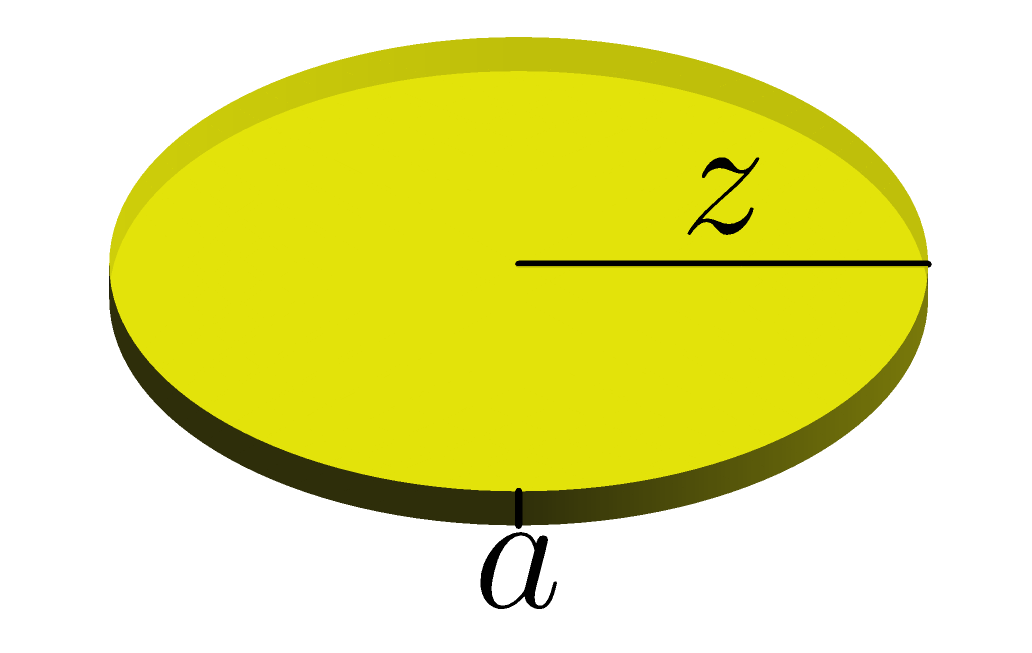
Med udgangspunkt i den fundne funktion, besvares følgende spørgsmål. Svarene på de to første spørgsmål kan med fordel angives i enheder af .
Find først arealet af den cirkel, som udgør pizzabundens top og bund.
Fun fact
Gang dernæst med tykkelsen for at finde rumfanget.
Bemærk at denne formel kan udtales pizza ().
- Hvor meget dej skal der bruges til en (Chicago style) pizza med en radius på 10 cm og en tykkelse på 1 cm?
- Hvor meget dej skal der bruges til en pizza (måske fra New York eller Napoli) med en radius på 20 cm og en tykkelse på 2 mm?
- Hvor mange gange flere dej skal der bruges hvis tykkelsen fordobles?
- Hvor mange gange flere dej skal der bruges hvis radius fordobles?
- Vis at og bestem værdien af .
Hvad er definitionsmængden for funktionen ?

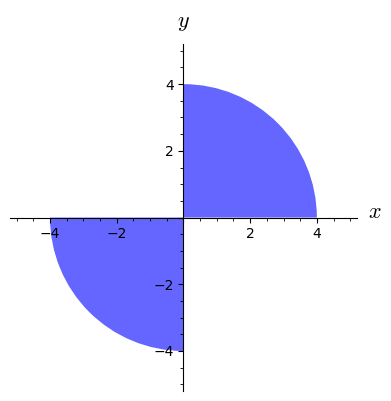


Hvad er definitionsmængden for funktionen ?
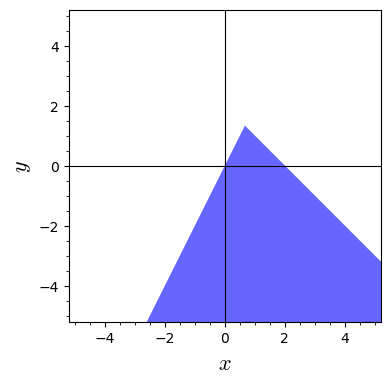


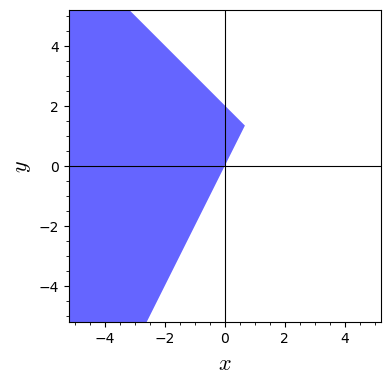
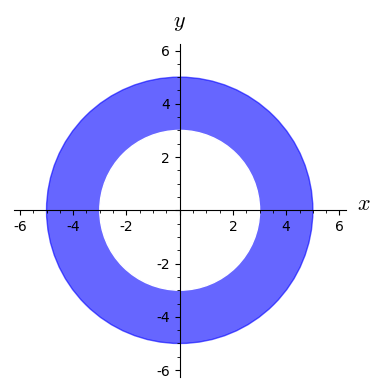
Hvilke(n) af nedenstående funktioner har den viste mængde som definitionsmængde?

En funktion af to variable er givet ved udtrykket
- Hvad er definitionsmængden for ?
- Skitsér definitionsmængden.
- Beregn funktionsværdierne og . Er de alle mulige at beregne? Hvis nej, hvorfor ikke?