9Uge 44

9.1 Pensum til denne uges forelæsning

Afsnit 18.2-18.5 i lærebogen.

9.2 Pensum til denne uges opgaver

Afsnit 17.5 og 18.1 i lærebogen.

9.3 Noter

Opskrift på at finde ekstrema (boks side 714)

Find alle kritiske punkter i $S$
Find maxima og minima på randen af $S$
Af disse punkter er det med størst funktionsværdi maksimum for $f$ i $S$ , og det med mindst funktionsværdi er minimum for $f$ i $S.$

Lagrange-multiplikatormetoden

For at finde max/min for $f(x,y)$ med bibetingelsen $g(x,y)=c$ :

Opstil ${\cal L} (x,y) = f(x,y) - \lambda \left( g(x,y)-c \right)$
Differentiér ${\cal L}$ mht $x$ og $y$ og sæt ${\cal L}'_1 = {\cal L}'_2 = 0$ .
Dette giver de tre ligninger:
${\cal L}'_1(x,y) = f'_1(x,y) - \lambda g'_1(x,y) = 0$
${\cal L}'_2(x,y) = f'_2(x,y) - \lambda g'_2(x,y) = 0$
$g(x,y) = c$
Løs disse for $(x,y,\lambda)$ . Disse er løsnings-kandidater.

9.4 Opgaver

Betragt følgende tre mængder:

$\begin{aligned} S_1 & = \{(x,y):5x^2+5y^2 \leq 9\} \\ S_2 & = \{(x,y):5x+8y>8\} \\ S_3 & = \{(x,y):2x+5y\geq8\} \end{aligned}$

Besvar følgende spørgsmål for hver af de tre mængder:

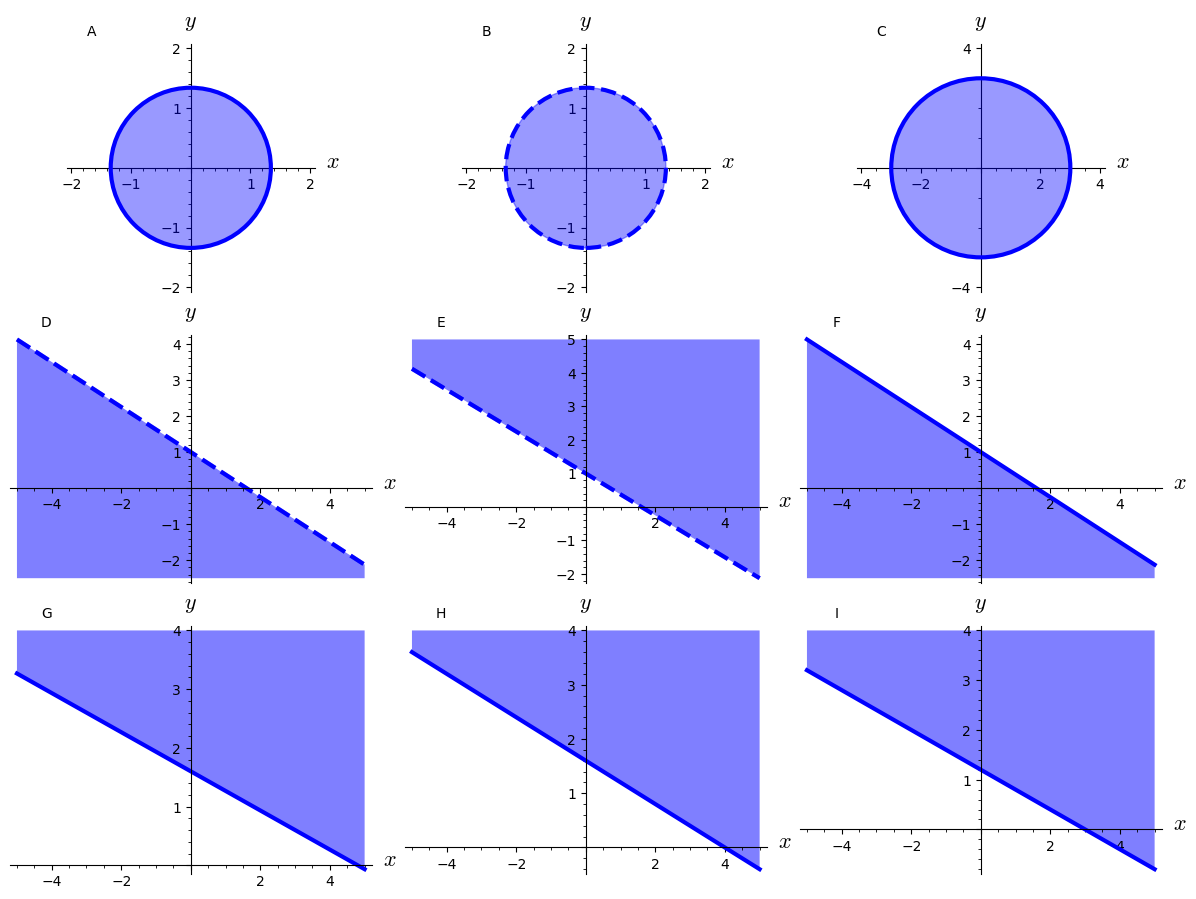
Hvilken af figurerne nedenfor svarer mængden til?
Er mængden åben eller lukket (eller hverken eller)?
Er mængden begrænset?
Er mængden kompakt?

Find det globale maksimum og minimum for følgende funktion i den givne definitionsmængde. Vi har:

$f(x,y) = x^2+5y^2$ hvor definitionsmængden er trekanten, der er afgrænset af linjerne $x=0$ , $y=0$ og $y+2x=2$ . Find også funktionsværdien i maksimums-punktet og minimums-punktet.

Find maksimums- og minimumspunkter for den følgende funktion:

$f(x,y)=x^2 +xy + y^2 -9x + 4$ inden for firkanten der er afgrænset af ulighederne $0\leq x\leq 7$ og $-4\leq y\leq 0$ .

Et maksimeringsproblem med bibetingelse er givet ved

$\text{max} \, f(x,y) = xy$ med bibetingelsen:

$x+y = 288$

Find den/de værdi(er) af $x$ og $y$ der løser problemet.

En funktion $f(x, y)$ har konturplottet vist nedenfor i figur A. Lysere områder svarer til højere funktionsværdier og mørkere områder svarer til lavere funktionsværdier.

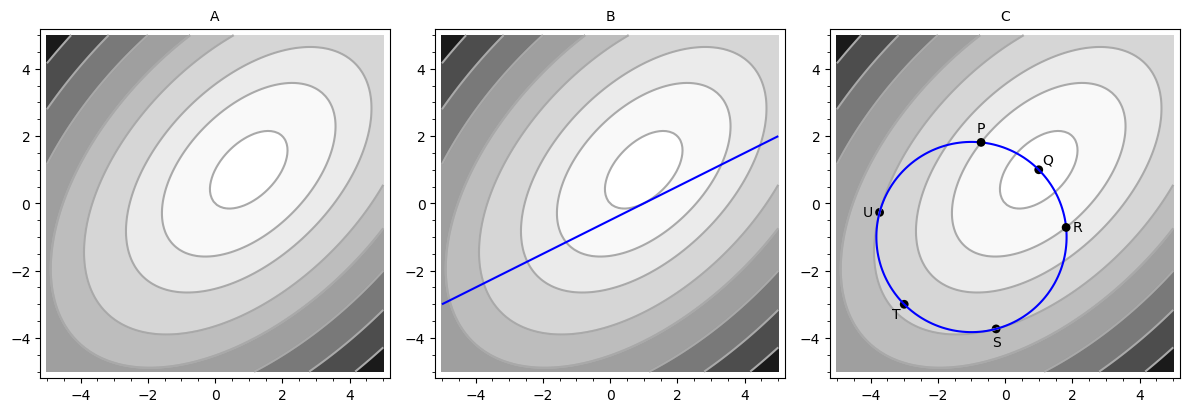
Angiv koordinaterne til punktet som maksimerer $f(x, y)$ . Aflæs punktet så godt du kan fra figuren.

I figur B er vist en bibetingelse, som den blå linje.

Angiv koordinaterne til punktet som maksimerer $f(x, y)$ under hensyn til bibetingelsen.

I figur C er vist en anden bibetingelse som en blå kurve, samt en række punkter. Besvar nedenstående ved at angive det eller de punkter der passer til det rigtige svar.

Hvor har funktionen makimum under hensyntagen til bibetingelsen?
Hvor har funktionen minimum under hensyntagen til bibetingelsen?

Brug Lagrange-multiplikatormetoden til at finde den maksimale værdi af $f(x,y)$ med den givne bibetingelse. Funktionen er givet ved

$f(x,y) = 30-x^2-y^2$ med bibetingelsen:

$x+5y = 26$

Et minimeringsproblem med bibetingelse er givet ved

$\text{min} \, f(x,y)=2x^2+4y^2$ med bibetingelsen:

$34-2x-3y=0$ Løs minimeringsproblemet.

En studerende har nyttefunktionen $u(x,y)=100xy+x+2y$ . Antag at prisen pr. kaffe $x$ er 10 kr. og at prisen på et måltid mad $y$ er 20 kr. Den studerende kan bruge 2000 kr. om måneden på kaffe og mad.

Løs nyttemaksimeringsproblemet.

(Tidligere eksamensopgave).

Et minimeringsproblem med bibetingelse er givet ved:

$\min f(x,y) = x^2+y^2$ hvor

$x^2y=2000$ Find den/de værdi(er) af $x$ og $y$ der løser problemet.

Hint: Kig evt. på afsnit 18.3 i bogen.