14Uge 49

14.1 Pensum til denne uges forelæsning

Afsnit 12.7, 13.1 og 13.6 i lærebogen.

14.2 Pensum til denne uges opgaver

Afsnit 12.1–12.3 og 12.5–12.6 i lærebogen.

14.3 Noter

Matrixoperationer

To matricer er lig hinanden hvis de har samme dimension og alle deres elementer er ens. Ellers er de forskellige.

$\begin{aligned} \mathbf{A} &= \mathbf{B} \quad\Longleftrightarrow\quad a_{ij} = b_{ij} \medspace \text{for alle kombinationer af} \medspace i, j\\ \mathbf{A} &\neq \mathbf{B} \quad\Longleftrightarrow\quad a_{ij} \neq b_{ij} \medspace \text{for mindst én kombination af} \medspace i, j \end{aligned}$

En sum af to matricer med samme dimension fås ved at lægge elementerne på samme plads sammen:

$\mathbf{C} = \mathbf{A} + \mathbf{B} \quad\Longleftrightarrow\quad c_{ij}=a_{ij}+b_{ij}$

Hvis $\mathbf{A}$ er en matrix med dimension $m\times n$ , og $\mathbf{B}$ er en matrix med dimension $n\times p$ , så defineres matrixproduktet $\mathbf{C=AB}$ ved:

$c_{ij} = \sum_{k=1}^n a_{ik}b_{kj}$

Regler for matrix multiplikation

$(\mathbf{A}\mathbf{B})\mathbf{C} = \mathbf{A}(\mathbf{B}\mathbf{C})$
$\mathbf{A}(\mathbf{B}+\mathbf{C}) = \mathbf{AB} + \mathbf{AC}$
$\mathbf{(A+B)C = AC+BC}$
$(\alpha\mathbf{A})\mathbf{B} = \mathbf{A}(\alpha\mathbf{B}) = \alpha\mathbf{AB}$

14.4 Opgaver

To matricer er givet ved:

$\textbf{A} = \begin{pmatrix} 0 & \phantom{-}2 \\ 1 & \phantom{-}3 \end{pmatrix}, \quad \textbf{B} = \begin{pmatrix} 1 & \phantom{-}4 \\ 5 & -4 \end{pmatrix}$

1. Udregn $\textbf{A}+\textbf{B}$ .

Dit svar: Det er en

2. Udregn $3\textbf{A}$ .

Dit svar: Det er en

To matricer er givet ved

$\textbf{A} = \begin{pmatrix} 4 & \phantom{-}3 & \phantom{-}1 \\ 8 & -2 & -6 \end{pmatrix}, \quad \textbf{B} = \begin{pmatrix} 0 & 4 & 6 \\ 2 & 5 & 9 \end{pmatrix}$

1. Udregn $\textbf{A}+\textbf{B}$ .

Dit svar: Det er en

2. Udregn $\textbf{A}-\textbf{B}$ .

Dit svar: Det er en

3. Udregn $4\textbf{A}-2\textbf{B}$ .

Dit svar: Det er en

Hvis det er muligt, udregn produkterne AB og BA, når A og B er defineret som:

$\textbf{A} = \begin{pmatrix} 0 & -2 \\ 3 & \phantom{-}1 \end{pmatrix}$ og $\textbf{B} = \begin{pmatrix} -1 & 4 \\ \phantom{-}1 & 5 \end{pmatrix}$
$\textbf{A} = \begin{pmatrix} 8 & 3 & -2 \\ 1 & 0 & \phantom{-}4 \end{pmatrix}$ og $\textbf{B} = \begin{pmatrix} 2 & -2 \\ 4 & \phantom{-}3 \\ 1 & -5 \end{pmatrix}$
$\textbf{A} = \begin{pmatrix} -1 & 0 \\ \phantom{-}2 & 4 \end{pmatrix}$ og $\textbf{B} = \begin{pmatrix} \phantom{-}3 & 1 \\ -1 & 1 \\ \phantom{-}0 & 2 \end{pmatrix}$
$\textbf{A} = \begin{pmatrix} \phantom{-} 0\\ -2 \\ \phantom{-}4 \end{pmatrix}$ og $\textbf{B} = \begin{pmatrix} 0 & -2 & 3 \end{pmatrix}$

To virksomheder, A og B, konkurrerer om markedsandele på telemarkedet. I starten har A en tredjedel af markedet og B har to tredjedele. Men danskerne skifter teleudbyder ret ofte, så i løbet af det næste år, og hvert efterfølgende år, sker der følgende:

A beholder 90% af sine kunder og mister 10% til B
B beholder 60% af sine kunder og mister 40% til A

Vi kan repræsentere markedsandelene af de to virksomheder med en markedsandels-vektor, som er givet som en søjlevektor $\mathbf{s}$ . Definitionen af en markedsandels-vektor er en søjlevektor med ikke-negative indgange der summer til 1. Vi definerer matricen $\mathbf{T}$ og den oprindelige markedsandels-vektor, $\mathbf{s}$ , som

$\displaystyle\textbf{T} = \begin{pmatrix} \displaystyle \frac{9}{10} & \displaystyle\frac{2}{5} \\[12pt] \displaystyle \frac{1}{10} & \displaystyle \frac{3}{5} \end{pmatrix}$ og $\displaystyle\textbf{s} = \begin{pmatrix} \displaystyle \frac{1}{3} \\[12pt] \displaystyle \frac{2}{3} \end{pmatrix}$

Bemærk at hvert element af $\mathbf{T}$ , $t_{ij}$ , er givet som andelen af $j$ 's kunder der bliver $i's$ kunder året efter. $\mathbf{T}$ er dermed en såkaldt overgangsmatrix.

Vis at $\mathbf{Ts}$ er en markedsandels-vektor.
Beregn $\mathbf{T}^2\mathbf{s}$ og fortolk dette matrixprodukt. Her er $\mathbf{T}^2\mathbf{s}$ det samme som $\mathbf{TTs}$ .

I et lands økonomi er der tre vigtige sektorer: $x, y$ og $z$ . For at kunne producere hvert deres output er disse sektorer afhængige af input fra de to andre sektorer og fra sektoren selv. Størrelsen på disse inputs og outputs mellem sektorerne i millarder er vist i nedenstående figur, som ikke medtager den del som eksporteres eller anvendes uden for de tre sektorer.

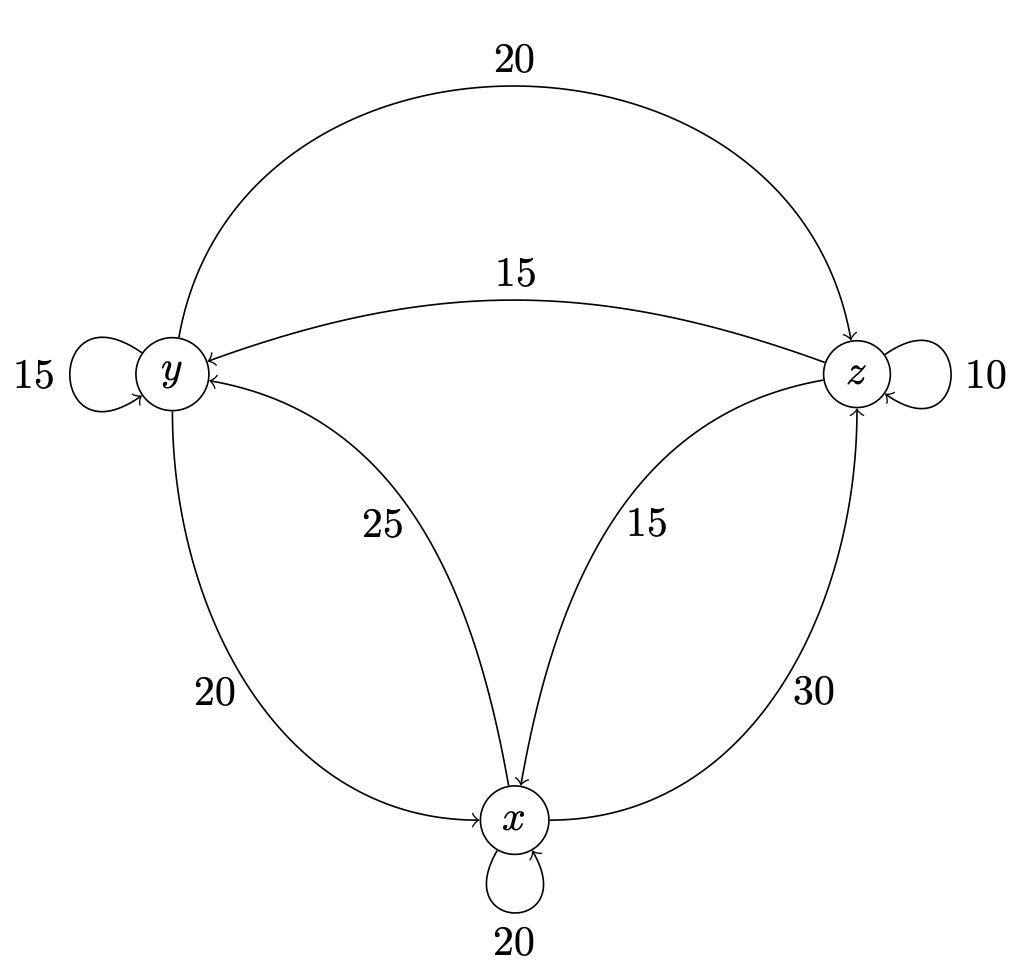
Opstil en matrix $\mathbf{B}$ hvor rækker og søjler svarer til $x$ , $y$ og $z$ og et element angiver hvor meget sektoren i rækken giver som input til sektoren i søjlen.

Skriv det følgende ligningssystem i matrix-form:

$\begin{aligned} 2x_1 - 5x_2 &= 3 \\ 5x_1 +8x_2 &= 5 \end{aligned}$

Skriv det følgende ligningssystem i matrix-form:

$\begin{aligned} x + y + z + t &= a \\ x + 3y + 2z + 4t &= b \\ x + 4y + 8z &= c \\ 2x + z - t &= d \end{aligned}$

(Tidligere eksamensopgave)

Lad et ligningssystem være:

$\begin{aligned} 3x_1 - x_2 - x_3 &= 5 \\ 2x_1 +x_2 - 2x_3 &= 0 \\ x_1 + 3x_2 + x_3 = 1 \end{aligned}$

Find A, x, og b, så ligningssystemet kan skrives som:
$\textbf{Ax}= \textbf{b}$
Find CA og AD, når $\textbf{C} = \begin{pmatrix} \phantom{-}7 & -2 & 3 \\ -4 & \phantom{-}4 & 4 \\ \phantom{-}5 & -10 & 5 \end{pmatrix}$ og $\textbf{D} = \begin{pmatrix} \phantom{-}5 & 24 & 28 \\ 20 & 12 & 24 \\ -5 & 20 & 0 \end{pmatrix}$

Tidligere eksamensopgave.

En virksomhed producerer tre produkter, A, B og C. Efterspørgslen på de tre produkter er funktioner af nogle markedsparametre (konstanter) $k_A$ , $k_B$ og $k_C$ samt priserne på de tre produkter $x_A$ , $x_B$ og $x_C$ . Disse efterspørgselsfunktioner er:

Produkt A: $\quad k_A - 2x_A + x_C$
Produkt B: $\quad k_B + 2x_A - 2x_B + 2x_C$
Produkt C: $\quad k_C + x_A + x_B - 2x_C$

Udbuddet af de tre produkter er givet ved følgende funktioner:

Produkt A: $\quad 3x_A -6$
Produkt B: $\quad x_B -9$
Produkt C: $\quad 2x_C - 9$

Opstil et system af ligninger, der udtrykker ligevægtsbetingelserne i markedet, altså hvor udbud er lig efterspørgsel for hvert af de tre produkter.
Bestem $\mathbf{A}$ , $\mathbf{x}$ og $\mathbf{b}$ så systemet af ligninger kan skrives på matrixform som
$\mathbf{Ax} = \mathbf{b}$

To matricer A og B er givet ved: $\textbf{A} = \begin{pmatrix*}[r] 3 & -5 & 7 \\ -3 & 1 & 2 \\ 4 & -9 & 4 \end{pmatrix*}$ og $\textbf{B} = \begin{pmatrix*}[r] 2 & 1 & 0 \\ 3 & 2 & -2 \\ 0 & 2 & -2 \end{pmatrix*}.$

1. Beregn AB.

Dit svar: Det er en

2. Beregn BA.

Dit svar: Det er en

Brug nedenstående matricer til at beregne $\textbf{C}(\textbf{A}-\textbf{B})$ .

$\textbf{A} = \begin{pmatrix} 2 & 5 & -4 \\ 4 & 0 & \phantom{-}9 \end{pmatrix}$ , $\textbf{B} = \begin{pmatrix} 1 & 6 & -4 \\ 3 & 7 & \phantom{-}0 \end{pmatrix}$ og $\textbf{C} = \begin{pmatrix} 4 & -6 \\ 2 & \phantom{-}1 \\ 4 & -7 \end{pmatrix}$

Dit svar: Det er en

(Tidligere eksamensopgave)

Lad $\textbf{A} = \begin{pmatrix} 5 & 3 \\ 0 & 5 \end{pmatrix}$ , $\textbf{B} = \begin{pmatrix} -8 & 0 & 7 \\ \phantom{-}1 & 3 & 2 \end{pmatrix}$ , og $\textbf{C} = \begin{pmatrix} 1 & 0 \\ 0 & 3 \\ 7 & 1 \end{pmatrix}$

Vis at $(\textbf{AB})\textbf{C} = \textbf{A}(\textbf{BC})$

Hvis A er en kvadratisk matrix, så er $\textbf{A}^2=\textbf{AA}$ . Lad: $\textbf{A} = \begin{pmatrix} 8 & 4 \\ 0 & 2 \end{pmatrix}$ . Find $\textbf{A}^2$ .

Dit svar: Det er en