15Uge 50

Find den transponerede af følgende matricer: $\textbf{A} = \begin{pmatrix} 3 & -8 \\ 1 & \phantom{-}6 \\ 4 & -9 \end{pmatrix}$, $\textbf{B} = \begin{pmatrix} 0 \\ 1 \\ 1 \\ 7 \end{pmatrix}$, og $\textbf{C} = \begin{pmatrix} 2 & -3 & 5 & 9 \end{pmatrix}$

Vis at matricerne $\textbf{A} = \begin{pmatrix} 3 & \phantom{-}2 & 3 \\ 2 & -1 & 1 \\ 3 & \phantom{-}1 & 0 \end{pmatrix}$ og $\textbf{B} = \begin{pmatrix} 0 & 4 & 8 \\ 4 & 0 & 13 \\ 8 & 13 & 0 \end{pmatrix}$ begge er symmetriske.

Danmark, Norge og Sverige har en del samhandel. Alle lande køber varer og tjenesteydelser af de andre (importerer) og sælger varer og tjenesteydelser til de andre (eksporterer).Deres samhandel kan udtrykkes med en matrix $\textbf{A}$, hvor $\textbf{A} = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}$Her betegner $a_{ij}$ hvor meget land $i$ eksporterer til land $j$ målt i milliarder kroner. Hvis f.eks. $a_{13}=5$ betyder det at land 1 eksporterer for 5 milliarder kroner til land 3.

1. Hvilke værdier har elementerne på diagonalen (hvor $i=j$) i $\textbf{A}$?
2. Er det rimeligt at antage at $\textbf{A}$ er symmetrisk? Begrund dit svar.
3. Handelsministeren i land 1 vil gerne have en søjlevektor med tre indgange, hvor den $i'te$ indgang er værdien af den samlede handel mellem land 1 og land $i$ (import + eksport). Hvilke(t) af de nedenstående udtryk giver en sådan vektor? Begrund dit svar.
   • $2\textbf{A}$
   • $\textbf{A}'$
   • $(\textbf{A} + \textbf{A}') \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$
   • $(\textbf{A} + \textbf{A}')$
   • $\textbf{A}\textbf{A}'$
   • $(\textbf{A} + \textbf{A}') \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix}$

Find værdien af determinanten: $\begin{vmatrix} 4 & 6 \\ 2 & 0 \end{vmatrix}$

Find værdien af determinanten: $\begin{vmatrix} 8 & 9 \\ 5 & 4 \end{vmatrix}$

Betragt følgende tre systemer af to ligninger med to ubekendte: $$\begin{aligned} 2x + 3y & = 3 \\ x - y & = - 1 \end{aligned}\tag{15.1}$$ $$\begin{aligned} 3x + 2y + 1 & = 0 \\ -\tfrac{3}{2}x - y & = - 2 \end{aligned}\tag{15.2}$$ $$\begin{aligned} y - \tfrac{2}{3}x & = 2 \\ 4x - 6y + 12 & = 0 \end{aligned}\tag{15.3}$$

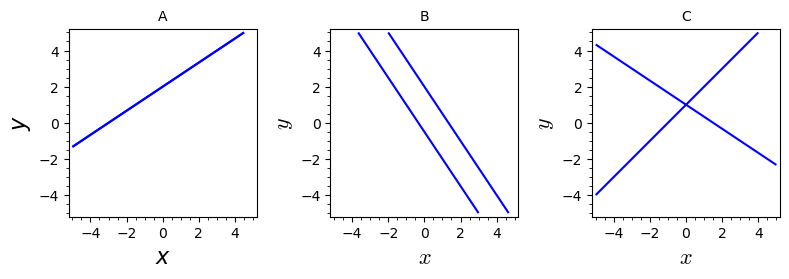
1. Opskriv hvert af de tre ligningssystemer på matrixform $\mathbf{Ax} = \mathbf{b}$.
2. Beregn for hvert af de tre ligningssystemer $\vert\mathbf{A}\vert$.
3. Angiv for hvert af de tre ligningssystemer det tilhørende plot nedenfor.
4. Hvor mange løsninger er der til hvert af de tre ligningssystemer?

Brug Cramers regel til at løse ligningerne (hvis muligt): $$\begin{aligned} 3x-8y & = 8 \\ x-2y & = 5 \end{aligned}$$

Brug Cramers regel til at løse ligningerne (hvis muligt): $$\begin{aligned} x+3y & = 1 \\ 3x-2y & = 14 \end{aligned}$$

(Tidligere eksamensopgave)Lad a og b være konstanter. Brug Cramers regel til at løse ligningerne for de to ubekendte variable, $x$ og $y$: $$\begin{aligned} ax-by & = 1 \\ bx+ay & = 2 \end{aligned}$$

(Tidligere eksamensopgave)Tre matricer $\mathbf{A}$, $\mathbf{B}$ og $\mathbf{C}$ er givet ved $$\mathbf{A} = \left(\begin{array}{rr} 0 & -1 \\ 1 & 0 \end{array}\right), \qquad \mathbf{B} = \left(\begin{array}{rr} -1 & 0 \\ 0 & -1 \end{array}\right), \qquad \mathbf{C} = \left(\begin{array}{rr} 0 & 1 \\ -1 & 0 \end{array}\right).$$

1. Vis at $\mathbf{AB} = \mathbf{C}$ og $\mathbf{BC} = \mathbf{A}$.
2. Beregn matrixproduktet $\mathbf{CA}$.

Matricerne $\mathbf{A}$, $\mathbf{B}$ og $\mathbf{C}$ er specialtilfælde af den generelle form $$\mathbf{D} = \left(\begin{array}{rr} {\alpha} & {\beta} \\ -{\beta} & {\alpha} \end{array}\right)$$ hvor $\alpha$ og $\beta$ er skalare konstanter (reelle tal).

3. Find værdierne af $\alpha$ og $\beta$, der sikrer at $\mathbf{D}$ opfylder ligningen $\mathbf{D}^2 = \mathbf{I}$, hvor $\mathbf{I}$ er identitetsmatricen.

En simpel model for at forudsige vejret bygger på sandsynligheden for regnvejr eller solskinsvejr i morgen givet vejret i dag. Antag, at hvis det er regnvejr i dag, er sandsynligheden for at det regner i morgen 70%, mens det omvendt gælder, at hvis det er solskinsvejr i dag, er sandsynligheden for solskinsvejr i morgen 60%.

1. Opstil en matrix $\mathbf{P}$ hvor første søjle svarer til at vejret i dag er regnvejr og anden søjle svarer til at vejret i dag er solskinsvejr. Første række svarer til at vejret i morgen er regnvejr og anden række svarer til at vejret i morgen er solskinsvejr. Et matrixelement i $\mathbf{P}$ er sandsynligheden for at vejret i morgen svarer til rækken, givet at vejret i dag svarer til søjlen.
   $$\textbf{P}= \begin{array}{rc} &\begin{array}{c}\text{regn i dag}\phantom{x}\text{sol i dag}\end{array}\\ \begin{array}{r}\text{regn i morgen}\\\text{sol i morgen}\end{array}\hspace{-1em} & \begin{pmatrix}\quad p_{11}\quad&\quad p_{12}\quad\\p_{21}&p_{22}\end{pmatrix}& \end{array}$$ Angiv sandsynlighederne som brøk eller decimaltal, ikke i procent. Decimaltal skal skrives med punktum, ikke komma. En sandsynlighed på 50% skal f.eks. skrives som 1/2 eller 0.5, ikke som 50 eller 0,5.
   Du kan antage at det hver dag enten er regnvejr eller solskin. Sandsynlighederne for disse udfald på en given dag skal derfor summere til 1 uanset om det dagen før var en regnvejrsdag eller en solskinsdag.
   Opstil $\mathbf{P}$.

   Dit svar: Det er en Skalar Søjlevektor Rækkevektor Matrix som er med 1 2 3 4 indgange med størrelse 1 2 3 4 x 1 2 3 4 givet ved Korrekt! Forkert.
2. Vejret i dag kan beskrives ved en søjlevektor, $\mathbf{w}$, som er en af disse:
   $$\text{regnvejr:}\, \begin{pmatrix}1\\ 0\end{pmatrix} \quad \text{solskinsvejr:}\, \begin{pmatrix}0\\ 1\end{pmatrix}.$$ Forklar hvorfor $\mathbf{Pw}$ kan tolkes som en vektor, der angiver sandsynligheden for vejret i morgen.
   Beregn $\mathbf{Pw}$ i det tilfælde hvor det er regnvejr i dag.

   Dit svar: Det er en Skalar Søjlevektor Rækkevektor Matrix som er med 1 2 3 4 indgange med størrelse 1 2 3 4 x 1 2 3 4 givet ved Korrekt! Forkert.
3. Hvilket udtryk angiver en søjlevektor, hvor elementerne er sandsynlighederne for hhv. regnvejr og solskinsvejr i overmorgen, når $\mathbf{w}$ er søjlevektoren for vejret i dag?
   Vælg blandt følgende svarmuligheder:

   $\mathbf{w'Pw}$

   $\mathbf{Pw^2}$

   $\mathbf{PwP}$

   $\mathbf{P^2w}$
   Check
4. Brug matrixmultiplikation til at beregne vektoren der udtrykker sandsynligheden for vejret i overmorgen, hvis det er regnvejr i dag. Til beregningerne kan det være en fordel at skrive matrixelementerne som brøker, altså f.eks. skrive $\frac{5}{10}$ i stedet for 0.5.
   Beregn matrixproduktet du fandt ovenfor.

   Dit svar: Det er en Skalar Søjlevektor Rækkevektor Matrix som er med 1 2 3 4 indgange med størrelse 1 2 3 4 x 1 2 3 4 givet ved Korrekt! Forkert.
5. Hvad er sandsynligheden for at det er solskinsvejr i overmorgen, hvis det er regnvejr i dag?
   Angiv svaret som brøk eller decimaltal.

   Dit svar: Det er en Skalar Søjlevektor Rækkevektor Matrix som er med 1 2 3 4 indgange med størrelse 1 2 3 4 x 1 2 3 4 givet ved Korrekt! Forkert.

En dansk virksomhed skal have sendt varer frem og tilbage med tog mellem en fabrik i Danmark og en fabrik i Sydeuropa. Varerne skal kvalitetstjekkes et sted i Tyskland indimellem transporten mellem Danmark og Sydeuropa.Fabrikken i Danmark kan ligge enten i Vejle eller Esbjerg. Varerne skal kvalitetstjekkes enten i Hamborg, Frankfurt eller Berlin. Fabrikken i Sydeuropa kan ligge enten i Bilbao, Toulouse, Milano eller Porto.Virksomheden er interesseret i at lægge fabrikkerne det sted hvor der er det størst mulige antal togforbindelser mellem byerne (givet et stop i en af de tyske byer).Antallet af togforbindelser mellem de danske byer og de tyske repræsenteres ved $2 \times 3$ matricen $\textbf{A}$, givet ved: $$\textbf{A}= \begin{array}{rc} &\begin{array}{c}\text{Berlin}\phantom{x}\text{Frankfurt}\phantom{x}\text{Hamborg} \end{array}\\ \begin{array}{r} \text{Esbjerg}\\ \text{Vejle} \end{array}\hspace{-1em} & \begin{pmatrix} \phantom{Be}0\phantom{lin} & \phantom{Fr}2\phantom{urt} & \phantom{Ha}1\phantom{org}\\ \phantom{Be}3\phantom{lin} & \phantom{Fr}3\phantom{urt} & \phantom{Ha}1\phantom{org} \end{pmatrix}& \end{array}$$ Her er der altså f.eks. $2$ togforbindelser mellem Esbjerg og Frankfurt men ingen mellem Esbjerg og Berlin.På samme måde repræsenterer $3 \times 4$-matricen $\textbf{B}$ togforbindelserne mellem de tyske byer og de sydeuropæiske byer: $$\textbf{B}= \begin{array}{rc} &\begin{array}{c}\text{Bilbao}\phantom{x}\text{Milano}\phantom{x}\text{Porto}\phantom{x}\text{Toulouse} \end{array}\\ \begin{array}{r} \text{Berlin}\\ \text{Frankfurt}\\ \text{Hamborg} \end{array}\hspace{-1em} & \begin{pmatrix} \phantom{Bi}2 & \phantom{Mil}3\phantom{no} & \phantom{P}0\phantom{to} & \phantom{T}1\phantom{use}\\ \phantom{Bl}4 & \phantom{Mil}1\phantom{no} & \phantom{P}2\phantom{to} & \phantom{T}3\phantom{use}\\ \phantom{Bi}0 & \phantom{Mil}2\phantom{no} & \phantom{P}1\phantom{to} & \phantom{T}2\phantom{use}\\ \end{pmatrix}& \end{array}$$ Der gælder nu at $\textbf{C}=\textbf{AB}$ betegner det totale mulige antal togforbindelser mellem de danske byer og de sydeuropæiske byer. $\textbf{C}$ er en $2 \times 4$-matrix givet ved: $$\textbf{C}= \begin{array}{rc} &\begin{array}{c}\text{Bilbao}\phantom{x}\text{Milano}\phantom{x}\text{Porto}\phantom{x}\text{Toulouse} \end{array}\\ \begin{array}{r} \text{Esbjerg}\\ \text{Vejle} \end{array}\hspace{-1em} & \begin{pmatrix} \phantom{Bi}\phantom{a} & \phantom{Mil}\phantom{a}\phantom{no} & \phantom{P}5\phantom{to} & \phantom{T}\phantom{a}\phantom{use}\\ \phantom{Bl}\phantom{a} & \phantom{Mi}14\phantom{no} & \phantom{P}\phantom{a}\phantom{to} & \phantom{T}\phantom{a}\phantom{use}\\ \end{pmatrix}& \end{array}$$ Altså er der f.eks. 5 måder at transportere varer mellem Esbjerg og Porto på.

1. Udfyld de manglende elementer i $\textbf{C}$
2. Hvor vælger virksomheden at lægge sine fabrikker?

Virksomheden hører nu rygter om at borgmestrene i Frankfurt og Milano overvejer at indsætte flere toge mellem deres byer. Virksomheden indser at de nye optimale placeringer af fabrikker nu måske bliver Vejle og Milano.

3. Hvor mange togforbindelser skal der mindst være mellem Frankfurt og Milano før det bliver optimalt at lægge fabrikkerne i Vejle og Milano i stedet for det svar du fik i 2)?

Vis at $\begin{pmatrix} 3 & \phantom{-}0 \\ 2 & -1 \end{pmatrix}^{-1} = \begin{pmatrix} 1/3 & \phantom{-}0 \\ 2/3 & -1 \end{pmatrix}$

Find den inverse til den pågældende matrix (hvis muligt): $\begin{pmatrix} 9 & 6 \\ 3 & 5 \end{pmatrix}$

Find den inverse til den pågældende matrix (hvis muligt): $\begin{pmatrix} 4 & -4 \\ 2 & -2 \end{pmatrix}$

Løs ligningerne ved at bruge den inverse matrix: $$\begin{aligned} 2x - 3y &= 3 \\ 3x - 4y &= 5 \end{aligned}$$

Løs ligningerne ved at bruge den inverse matrix: $$\begin{aligned} 4x_1 + 5x_2 &= 9 \\ 4x_1 + 8x_2 &= 24 \end{aligned}$$

(Tidligere eksamensopgave)Betragt følgende ligningssystem $$\begin{aligned} 3x_1 - x_2 - x_3 &= 5 \\ 2x_1 +x_2 - 2x_3 &= 0 \\ x_1 + 3x_2 + x_3 = 1 \end{aligned}$$

1. Bestem A, x, og b, så systemet af ligninger kan skrives på matrixform som:
   $$\textbf{Ax}= \textbf{b}$$ (Bemærk at du har lavet denne underopgave i opgave 14.8).
2. Beregn CA og AD, hvor $\textbf{C} = \begin{pmatrix} \phantom{-}7 & -2 & 3 \\ -4 & \phantom{-}4 & 4 \\ \phantom{-}5 & -10 & 5 \end{pmatrix}$ and $\textbf{D} = \begin{pmatrix} \phantom{-}5 & 24 & 28 \\ 20 & 12 & 24 \\ -5 & 20 & 0 \end{pmatrix}$
   (Bemærk at du har lavet denne underopgave i opgave 14.8).
3. Bestem skalaren $\alpha$ så $\alpha\textbf{C} = \mathbf{A}^{-1}$ (Hint: Benyt at $\mathbf{A}^{-1}\mathbf{A} = \mathbf{I}$).
4. Find den vektor $\mathbf{x}$ som er løsning til matrixligningen $\mathbf{Ax}=\mathbf{b}$.

(Tidligere eksamensopgave)En vektor $\mathbf{v}$ og to matricer $\mathbf{U}$ og $\mathbf{W}$ er givet ved $$\mathbf{U} = \begin{pmatrix} 1 & \sqrt{2} \\ \sqrt{2} & 1 \end{pmatrix}, \qquad \mathbf{v} = \begin{pmatrix} x \\ y \end{pmatrix}, \qquad \mathbf{W} = \begin{pmatrix} w_{11} & w_{12} \\ w_{21} & w_{22} \end{pmatrix},$$ hvor elementerne i $\mathbf{v}$ er reelle variable og elementer i $\mathbf{W}$ er reelle konstanter.

1. Find den inverse matrix til $\mathbf{U}$.
2. Beregn $\mathbf{v'Wv}$, hvor $\mathbf{v'}$ er den transponerede til $\mathbf{v}$.
3. Antag at $\mathbf{W}$ er symmetrisk og bestem $\mathbf{W}$ (dvs. alle elementerne i $\mathbf{W}$), så der gælder at
   $$\mathbf{v'Wv} = (x - y)^2.$$