3Uge 38

3.1 Pensum til denne uges forelæsning

Sektion 7.3, 7.12 og 14.1 i lærebogen.

3.2 Pensum til denne uges opgaver

Sektion 6.8 – 6.11 og 8.5 i lærebogen.

3.3 Noter

Leibnizs notation

I Leibnizs notation skriver vi differentialkvotienten $f'(x)$ af en funktion $y = f(x)$ på en af følgende måder:

$f'(x) = \frac{\mathrm{d}f}{\mathrm{d}x} = \frac{\mathrm{d}y}{\mathrm{d}x}$

Regler for differentiation

Med Leibnizs notation ser reglerne for at differentiere en sum/differens, et produkt og en kvotient af to funktioner således ud:

$\begin{aligned} {}& \frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \left( f(x)\pm g(x) \right) = \frac{\mathrm{d}f}{\mathrm{d}x} \pm \frac{\mathrm{d}g}{\mathrm{d}x} \\[3ex] {}& \frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \left( f(x)\cdot g(x) \right) = \frac{\mathrm{d}f}{\mathrm{d}x} \cdot g(x) + f(x)\cdot \frac{\mathrm{d}g}{\mathrm{d}x} \\[3ex] {}& \frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \left( \frac{f(x)}{g(x)} \right) = \frac{ \frac{\mathrm{d}f}{\mathrm{d}x} \cdot g(x) - f(x)\cdot \frac{\mathrm{d}g}{\mathrm{d}x}} {\left( g(x) \right)^2} \end{aligned}$

I notationen med mærker, ser reglerne således ud

$\begin{aligned} {}& F(x) = f(x)\pm g(x) \quad\Longrightarrow\quad F'(x) = f'(x)\pm g'(x)\\ {}& F(x) = f(x)\cdot g(x) \quad\Longrightarrow\quad F'(x) = f'(x)g(x) + f(x)g'(x)\\ {}&F(x) = \frac{f(x)}{g(x)} \quad\Longrightarrow\quad F'(x) = \frac{f'(x) g(x) - f(x) g'(x)}{\left( g(x) \right)^2} \end{aligned}$

Kædereglen

For en sammensat funktion $F(x) = f(g(x))$ gælder med $y=f(u)$ og $u=g(x)$ kædereglen for differentialkvotienten:

$\begin{aligned} F'(x) &= f'(g(x)) \, g'(x) \\[3ex] \frac{\mathrm{d}y}{\mathrm{d}x} &= \frac{\mathrm{d}y}{\mathrm{d}u}\frac{\mathrm{d}u}{\mathrm{d}x} \end{aligned}$

Højere ordens afledede

$\begin{aligned} f''(x) &= \frac{\mathrm{d}^2f}{\mathrm{d} x^2} \\ f^{(3)}(x) &= \frac{\mathrm{d}^3f}{\mathrm{d} x^3} \\ & \dots \\ f^{(n)}(x) &= \frac{\mathrm{d}^nf}{\mathrm{d} x^n} \end{aligned}$

3.4 Opgaver

I denne opgave kigger vi på hvordan en formue udvikler sig efter man har investeret et vist beløb som forrentes med kontinuert rentetilskrivning.

Lad $F(t) = Be^{rt}$ betegne formue som funktion af tid $t$ målt i år siden investeringen, hvor $B$ er den investerede startformue i millioner kroner og $r$ er rentesatsen i decimaltal. Dvs. fx. hvis renten er 15%, da er $r=0.15$ .

Det er helt fint at angive svar i termer af $e$ . Dvs. et svar kunne hypotetisk godt være fx $5e$ , eller fx $\frac{1}{2}e^{0.2}$

Hvis startformuen er 2 millioner kroner og renten er 10%, hvad er da formuen efter 10 år?
Hvad er formuens ændringshastighed efter 10 år?

Beregn nedenstående differentialkvotienter:

$\displaystyle \frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \frac{e^x - 1}{x^2}$
$\displaystyle \frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \left( x^2 + \ln(x^2) \right)$
$\displaystyle \frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \frac{\ln x}{x}$
$\displaystyle \frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \frac{x}{\ln x}$
$\displaystyle \frac{\mathrm{d}\phantom{y}}{\mathrm{d}y} \left( e^{y} \cdot \ln y \right)$
$\displaystyle \frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} e^{-2x^3-4x}$

Find den afledede af nedenstående funktioner både med og uden brug af kædereglen.

$f(x) = \ln(x^5)$
$g(x) = (x^2-2)^2$

Hvad er nemmest i hvert af de to tilfælde?

Beregn $\frac{\mathrm{d}y}{\mathrm{d}x}$ hvor $y = \sqrt{u}$ og $u = 3x^2 + \tfrac{1}{2}x$ .

Benyt kædereglen til at beregne nedenstående differentialkvotienter.

$\displaystyle\frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} (-x^3 + 7x + 5)^9$ .
$\displaystyle\frac{\mathrm{d}\phantom{t}}{\mathrm{d}t} 5(-3t^3 + 7t)^{-5}$ .
$\displaystyle\frac{\mathrm{d}\phantom{x}}{\mathrm{d}x} \frac{-3}{(x-3x^2)^3}$ .

En variabel $z$ er en funktion af en anden variabel $q$ , som igen er en funktion af variablen $t$ . Sammenhængen er givet ved følgende relationer

$z = p(q) \qquad q = w(t).$ Opskriv nu kædereglen i Leibnizs notation og mærkenotationen ved at trække det korrekte indhold op i kasserne.

$\displaystyle\frac{\mathrm{d} z}{\mathrm{d} t} = \,$

$\,\cdot\,$

$z'(t) = \,$

$\Bigg($

$\Bigg)$ $\,\cdot\,$

$\Bigg($

$\Bigg)$

$p$

$z$

$t$

$\displaystyle\frac{\mathrm{d} z}{\mathrm{d} p}$

$\displaystyle\frac{\mathrm{d} p}{\mathrm{d} q}$

$\displaystyle\frac{\mathrm{d} q}{\mathrm{d} t}$

$w(t)$

$p'$

$w'$

Find $f'(x)$ , $f''(x)$ og $f^{(3)}(x)$ for funktionen $f(x) = 3x^3 - 5x^2 + 27.$

Beregn nedenstående differentialkvotienter.

$f''(x)$ , hvor $f(x) = x^2 e^{-2x}$
$g''(y)$ , hvor $g(y) = (1-3y^3)^7$
$\displaystyle\frac{\mathrm{d}^2y}{\mathrm{d}x^2}$ , hvor $y = \sqrt[6]{x}$

Lad $f(t)$ betegne Mærsks omsætning i år $t$ .

Forbind udsagnene nedenfor med de korrekte matematiske udtryk ved at trække de matematiske udtryk op i de kasser der passer til udsagnene.

a) Omsætningen er faldende, men tempoet i faldet er aftagende

b) Omsætningen vokser, og den vokser mere og mere som tiden går

c) Omsætningen vokser, men den vokser mindre og mindre som tiden går

d) Omsætningen er faldende, og tempoet i faldet er voksende

$f'(t)>0$ og $f''(t)>0$

$f(t)=0$ og $f'(t)<0$

$\frac{df}{dt}<0$ og $\frac{d^2f}{dt^2}>0$

$f'(t)<0$ og $f''(t)<0$

$f'(t)>0$ og $f''(t)<0$

En funktion $u$ er givet ved: $u(v) = \sqrt{v^2 + 1}$ .

Hvad er $\displaystyle\frac{\mathrm{d} u}{\mathrm{d} v}$ ?

Svaret kan skrives på flere måder. Forsøg at udtrykke dit svar ved $u$ og $v$ og gøre det så simpelt som muligt.

$\frac{v}{u}$

$uv$

$\frac{1}{2u}$

$\frac{\sqrt{v}}{2u}$

Hvad er $\displaystyle\frac{\mathrm{d}^2 u}{\mathrm{d} v^2}$ ?

Svaret kan skrives på flere måder, og det kræver lidt omskrivning at finde det rigtige udtryk. Benyt evt. relationen $u = \sqrt{v^2 + 1}$ til at udtrykke $u^2$ ved $v$ efter du har differentieret og simplificeret udtrykket.

$\frac{uv - vu'}{u^2}$

$\frac{u - vu}{u^2}$

$\frac{1}{u^3}$

$\frac{{u^2-v^2}}{u^2}$

Nedenfor er vist grafer med forskellige kombinationer af fortegnene på 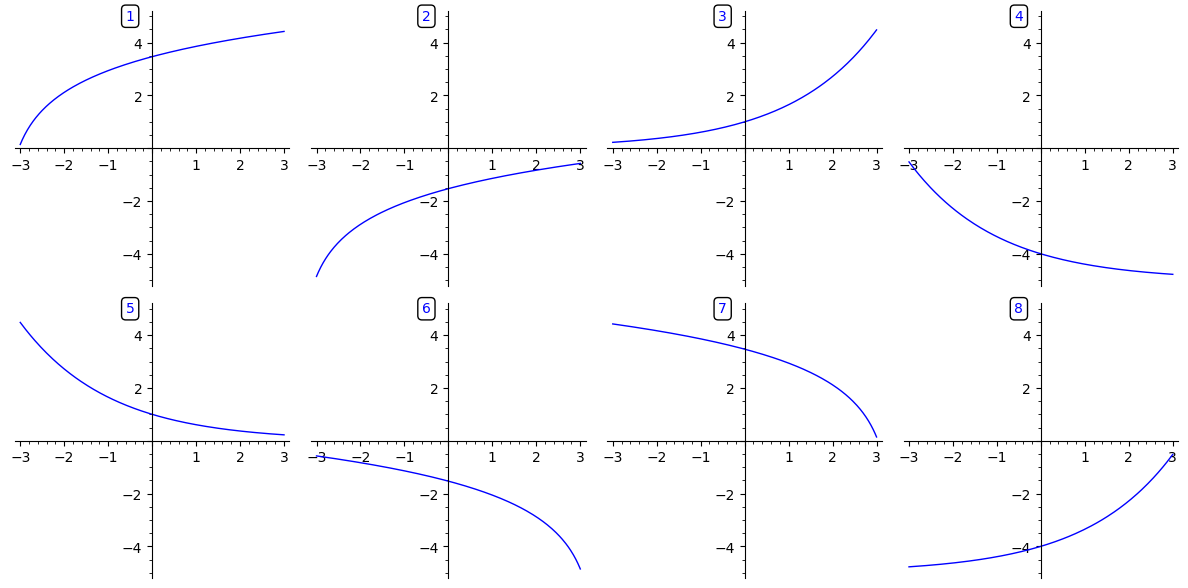$f(x)$ , $f'(x)$ og $f''(x)$ .

Træk tallene svarende til graferne op i de tomme kasser, så de passer til fortegnene på $f(x)$ , $f'(x)$ og $f''(x)$ .

$f(x) > 0$ , $f'(x) > 0$ , $f''(x) > 0$

$f(x) > 0$ , $f'(x) > 0$ , $f''(x) < 0$

$f(x) > 0$ , $f'(x) < 0$ , $f''(x) > 0$

$f(x) > 0$ , $f'(x) < 0$ , $f''(x) < 0$

$f(x) < 0$ , $f'(x) > 0$ , $f''(x) > 0$

$f(x) < 0$ , $f'(x) > 0$ , $f''(x) < 0$

$f(x) < 0$ , $f'(x) < 0$ , $f''(x) > 0$

$f(x) < 0$ , $f'(x) < 0$ , $f''(x) < 0$