7Uge 42

7.1 Pensum til denne uges forelæsning

Afsnit 14.7-14.8 og 17.2-17.3 i lærebogen.

7.2 Pensum til denne uges opgaver

Sektion 15.3 og 17.1 i lærebogen.

7.3 Noter

Hældningen på en niveaukurve

Hvis $F(x,y)=c$ og $F_2'(x,y) \neq 0$ , da gælder

$y' = - \frac{F_1'(x,y)}{F_2'(x,y)}$

Teorem 17.1.1

En differentiabel funktion $z=f(x,y)$ kan kun have et maksimum eller minimum i et indre punkt $(x_0, y_0)$ af sin definitionsmængde hvis det er et kritisk punkt - dvs. hvis punktet $(x,y)=(x_0,y_0)$ opfylder de to ligninger

$f_1'(x,y) = 0$

$f_2'(x,y) = 0$ hvilket også kaldes førsteordensbetingelserne, eller FOCs.

7.4 Opgaver

Brug den generelle kæderegel til at finde $\frac{\partial w}{\partial t}$ og $\frac{\partial w}{\partial s}$ for:

$w=2xy^2z^2 + yz$ hvor $x=t^2$ , $y=s$ og $z=t-s$

En funktion af to variable, hvor $y$ er defineret som en differentiabel funktion af $x$ , er givet ved:

$6x^3-8y^2+2xy = 0$ Find $\frac{dy}{dx}$ ved at bruge formlen i noterne.

En funktion af to variable er givet ved:

$F(x,y) = 4xe^{3y}-5x^2y^3$ Brug formlen $\frac{dy}{dx} = -\frac{F'_1(x,y)}{F'_2(x,y)}$ til at finde hældningen for niveaukurven for $F(x,y) = 4$ i punktet $(1,0)$ .

Efterspørgslen $x$ er antallet af vinterjakker, der kan blive solgt til prisen $p$ . For:

$x=2p^3-4p^2+1000$ find den øjeblikkelige tilvækst af $p$ mht. $x$ ved at differentiere implicit.

I denne opgave møder vi Dorthe. Træk et udtryk fra de nederste kasser op i den tomme kasse, så sætningen kommer til at passe.

Dorthe bor i Aarhus. Det er

for at hun bor i Jylland

en nødvendig betingelse

en tilstrækkelig betingelse

ikke en tilstrækkelig betingelse

I denne opgave møder vi Dylan. Træk et udtryk fra de nederste kasser op i den tomme kasse, så sætningen kommer til at passe.

Dylan bor i Jylland. Det er

for at han bor i Aarhus

ikke en nødvendig betingelse

en tilstrækkelig betingelse

en nødvendig betingelse

Find alle kritiske punkter af $f(x,y)$ for:

$f(x,y) = x^2 - 4xy+3y^2+6x-8y-8$

Find alle punkter $(x,y)$ hvor $f(x,y)$ kan have et maksimum eller minimum:

$f(x,y) = -4x^2+10xy+3y^2+x-y$

(Del af tidligere eksamensopgave)

Lad funktionen $f$ være givet ved:

$f(x, y) = (x-y)^2 -2x -y(3y - 1 -x) + 7$

Find første og anden ordens afledte af funktionen $f$ .
Undersøg om funktionen $f$ har et indre stationært (kritisk) punkt.

Find alle kritiske punkter af $f(x,y)$ for:

$f(x,y) = \frac{1}{3}x^3-4y^3-3x+12y-1$

Betragt funktionen $h(x,y) = -x^3 + y^3 + 2x - 3y$ .

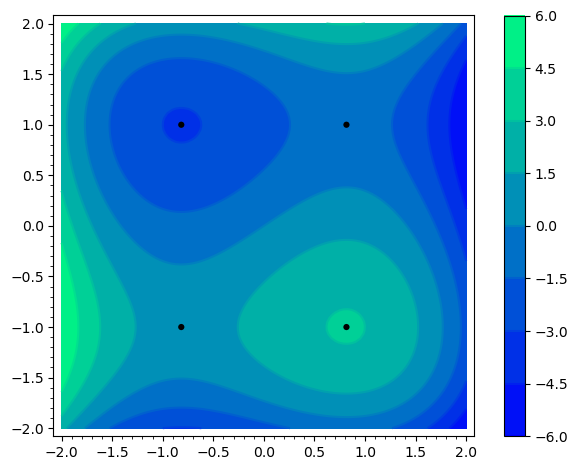
Vis at $h$ har de kritiske punkter $(x, y) = \left(-\sqrt{2/3} , 1\right),$ $\left(\sqrt{2/3} , 1\right),$ $\left(-\sqrt{2/3} , -1\right),$ $\left(\sqrt{2/3} , -1\right)$
Bestem ud fra konturplottet nedenfor hvilke af disse punkter, der er et maksimum eller et minimum.

PostNord kræver, at enhver pakke må have en længde plus omkreds, der maksimalt er 300 cm. Vi kalder bredden for $x$ , højden for $y$ og længden for $z$ , som i figuren nedenfor.

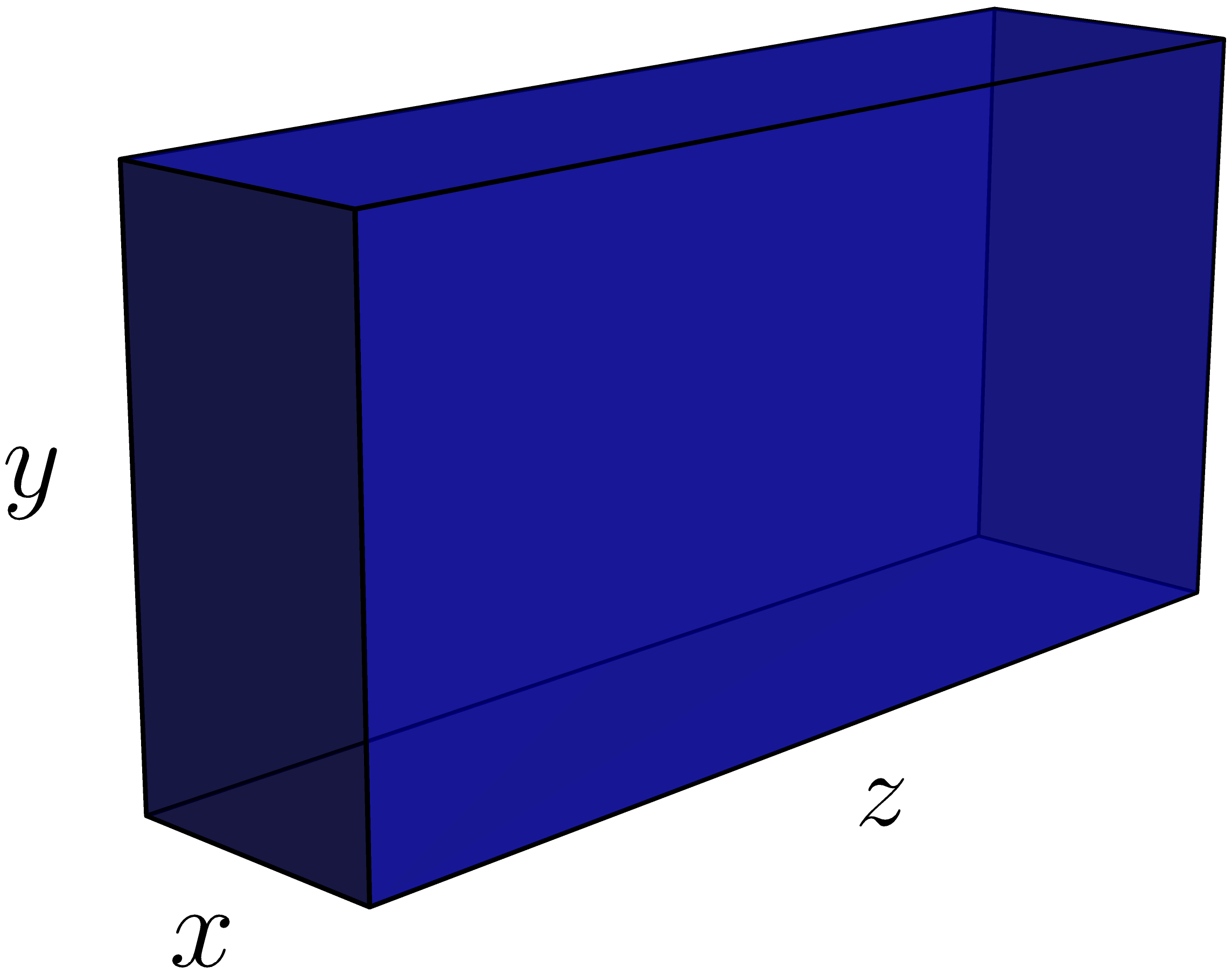
Find dimensionerne på pakken med det maksimale volumen, som kan sendes.

Udtryk volumen, længde og omkreds ved $x$ , $y$ og $z$ .

For det maksimale volumen gælder at $300 \,\mathrm{cm}=$ længde + omkreds $= z + (2x + 2y)$ . Brug dette til at eliminere $z$ fra udtrykket for $V$ , som så kan skrives som en funktion af $x$ og $y$ . Find nu det kritiske punkt, som kan antages at være et maksimum.
PostNord kræver yderligere, at længden maksimalt må være 150 cm. Er dette krav opfyldt i den fundne løsning?

Antag at et firmas årlige profit er givet ved:

$P(x,y) = -2x^2 - 3y^2 + 12x+4y + 10$ hvor $x$ og $y$ betegner, hvor meget der bruges på henholdsvis produktudvikling og marketing (i millioner kroner).

Find firmaets profit, når $x=\frac{1}{2}$ og $y=1$ .
Find alle de mulige værdier af $x$ og $y$ , der kan maksimere profitten, og udregn hvad profitten i givet fald vil være.